Given two strike prices \(K_{1}- One long call with strike price \(K_{1}\) and payoff function \(\left(x-K_{1}ight)^{+}\),
- One short put with strike price \(K_{1}\) and payoff function \(-\left(K_{1}-xight)^{+}\),
- One short call with strike price \(K_{2}\) and payoff function \(-\left(x-K_{2}ight)^{+}\),
- One long put with strike price \(K_{2}\) and payoff function \(\left(K_{2}-xight)^{+}\).

The risk-free interest rate is denoted by \(r \geqslant 0\).

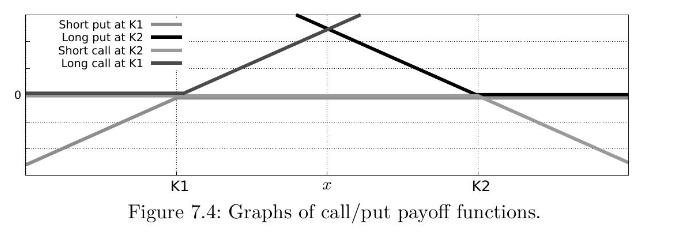
a) Find the payoff of the long box spread option in terms of \(K_{1}\) and \(K_{2}\).
b) Price the long box spread option at times \(k=0,1, \ldots, N\) using \(K_{1}, K_{2}\) and the interest rate \(r\).
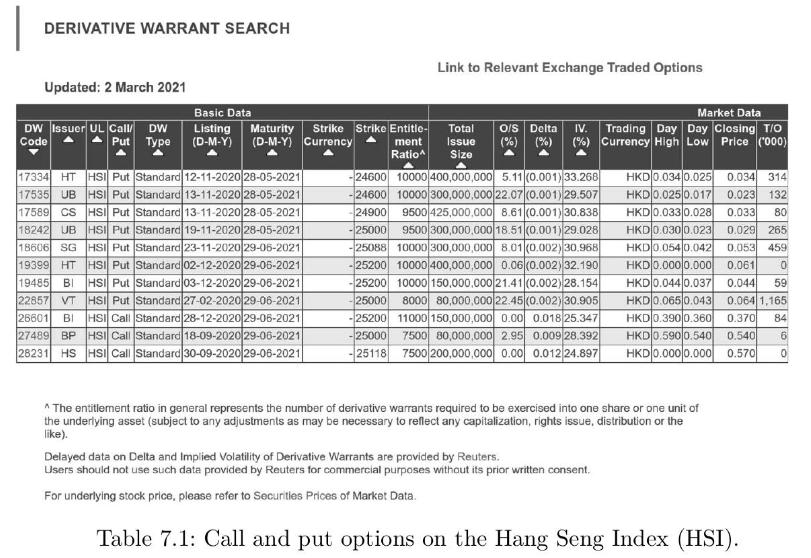
c) From Table 7.1 below, find a choice of strike prices \(K_{1}
d) Price the option built in part (c) in index points, and then in \(\mathrm{HK} \$\).
Hints.
i) The closing prices in Table 7.1 are warrant prices quoted in index points.
ii) Warrant prices are converted to option prices by multiplication by the number given in the "Entitlement Ratio" column.
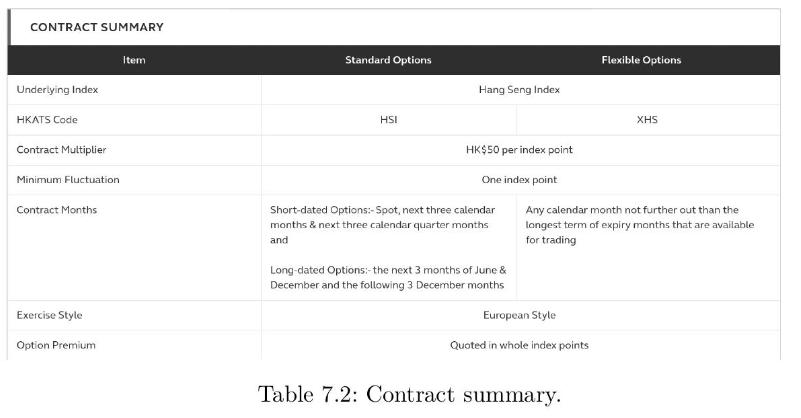
iii) The conversion from index points to \(\mathrm{HK} \$\) is given in Table 7.2.
e) Would you buy the option priced in part (d) ? Here we can take \(r=0\) for simplicity.

Transcribed Image Text:

0 Short put at K1 Long put at K2 Short call at K2 Long call at K1 K1 K2 Figure 7.4: Graphs of call/put payoff functions. I