On December 18, 2007, a call warrant has been issued by Fortis Bank on the stock price \(S\) of the MTR Corporation with maturity \(T=23 / 12 / 2008\), strike price \(K=\) HK\$ 36.08 and entitlement ratio \(=10\). Recall that in the Black-Scholes model, the price at time \(t\) of the European claim on the underlying asset priced \(S_{t}\) with strike price \(K\), maturity \(T\), interest rate \(r\) and volatility \(\sigma>0\) is given by the Black-Scholes formula as
\[
f\left(t, S_{t}ight)=S_{t} \Phi\left(d_{+}(T-t)ight)-K \mathrm{e}^{-(T-t) r} \Phi\left(d_{-}(T-t)ight),
\]
where
\[
\left\{\begin{array}{l}
d_{-}(T-t)=\frac{\left(r-\sigma^{2} / 2ight)(T-t)+\log \left(S_{t} / Kight)}{|\sigma| \sqrt{T-t}}, \\
d_{+}(T-t)=d_{-}(T-t)+|\sigma| \sqrt{T-t}=\frac{\left(r+\sigma^{2} / 2ight)(T-t)+\log \left(S_{t} / Kight)}{|\sigma| \sqrt{T-t}} .
\end{array}ight.
\]
we have
\[
\frac{\partial f}{\partial x}\left(t, S_{t}ight)=\Phi\left(d_{+}(T-t)ight), \quad 0 \leqslant t \leqslant T
\]

we have

\[ \frac{\partial f}{\partial x}\left(t, S_{t}ight)=\Phi\left(d_{+}(T-t)ight), \quad 0 \leqslant t \leqslant T \]

a) Using the values of the Gaussian cumulative distribution function, compute the BlackScholes price of the corresponding call option at time \(t=\) November 7,2008 with \(S_{t}=\) HK\$ 17.200, assuming a volatility \(\sigma=90 \%=0.90\) and an annual risk-free interest rate \(r=4.377 \%=0.04377\),

b) Still using the Gaussian cumulative distribution function, compute the quantity of the risky asset required in your portfolio at time \(t=\) November 7, 2008 in order to hedge one such option at maturity \(T=23 / 12 / 2008\).

c) Figure 1 represents the Black-Scholes price of the call option as a function of \(\sigma \in\) \([0.5,1.5]=[50 \%, 150 \%]\).

Data from Figure 1

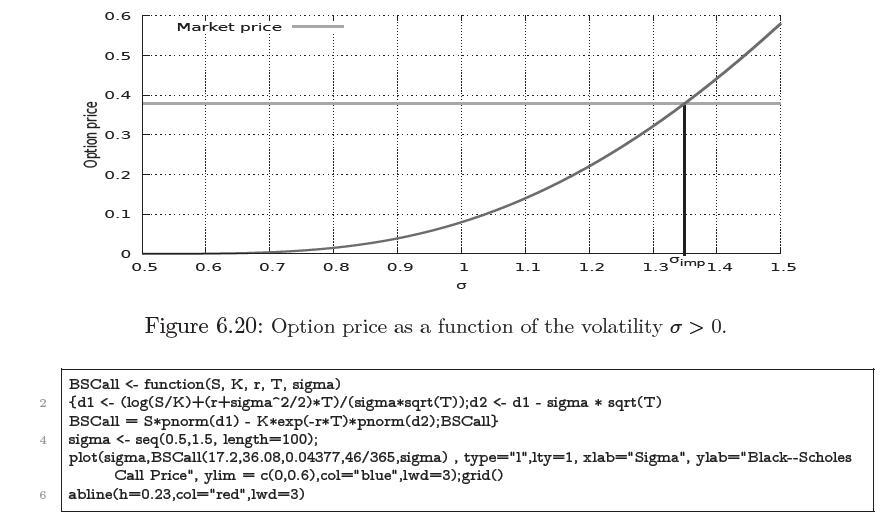
Knowing that the closing price of the warrant on November 7, 2008 was HK\$0.023, which value can you infer for the implied volatility \(\sigma\) at this date?

Transcribed Image Text:

2 4 6 Option price 0.6 0.5 0.4 0.3 0.2 0.1 O 0.5 Market price 0.6 0.7 0.8 0.9 1 O 1.1 1.2 S*pnorm(d1) - K*exp(-r*T)*pnorm(d2); BSCall) 1.3 Oimp1.4 Figure 6.20: Option price as a function of the volatility o> 0. 1.5 BSCall