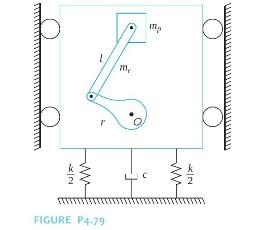
A schematic of a single-cylinder engine mounted on springs and a viscous damper is shown in Figure P4.79. The crank rotates about \(O\) with a constant speed \(\omega\). The connecting rod of mass \(m_{r}\) connects the crank and the piston of mass \(m_{p}\) such that the piston moves in a vertical plane. The center of gravity of the crank is at its axis of rotation.

(a) Derive the differential equation governing the absolute vertical displacement of the engine including the inertia forces of the crank and piston, but ignoring forces due to combustion. Use an exact expression for the inertia forces in terms of \(m_{r}, m_{p}, \omega\), the crank length \(r\), and the connecting rod length \(l\).

(b) Since \(F(t)\) is periodic, a Fourier series representation can be used. Set up, but do not evaluate, the integrals required for a Fourier series expansion for \(F(t)\).

(c) Assume \(r / l \ll 1\). Rearrange \(F(t)\) and use a binomial expansion such that \[ F(t)=\sum_{i=1}^{\infty} a_{i}\left(\frac{r}{l}\right)^{i} \]

(d) Truncate the preceding series after \(i=3\). Use trigonometric identities to approximate \[ F(t) \approx b_{1} \cos \omega t+b_{2} \cos 2 \omega t+b_{3} \cos 3 \omega t \]

(e) Find an approximation to the steady-state form of \(x(t)\).

Transcribed Image Text:

22 FIGURE P4-79 Mp *|2