A two degree of freedom spring-mass system is displayed in Fig. P4.5. For harmonic free vibration, complete the following if \(k_{1}=2 \times 10^{6} \mathrm{~N} / \mathrm{m}\), \(m_{1}=0.8 \mathrm{~kg}, k_{2}=1 \times 10^{6} \mathrm{~N} / \mathrm{m}\), and \(m_{2}=1.4 \mathrm{~kg}\). The initial displacements for the system's free vibration are \(x_{1}(0)=2 \mathrm{~mm}\) and \(x_{2}(0)=1 \mathrm{~mm}\) and the initial velocities are \(\dot{x}_{1}(0)=0 \mathrm{~mm} / \mathrm{s}\) and \(\dot{x}_{2}(0)=5 \mathrm{~mm} / \mathrm{s}\).
(a) Calculate the two natural frequencies and mode shapes. Normalize the mode shapes (eigenvectors) to coordinate \(x_{2}\).
(b) Define the modal matrix and determine the modal mass and stiffness matrices.
(c) Write the uncoupled single degree of freedom time responses for the modal coordinates \(q_{1}\) and \(q_{2}\). Use the following form: \(q_{1,2}(t)=A_{1,2} \cos \left(\omega_{n_{1,2}} t\right)+\) \(B_{1,2} \sin \left(\omega_{n_{1,2}} t\right)\) with units of \(\mathrm{mm}\).

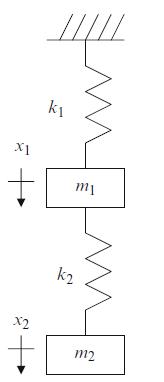
Fig. P4.5 Two degree of freedom spring-mass system.

(d) Write the time responses for the local coordinates \(x_{1}\) and \(x_{2}\) (in \(\mathrm{mm}\) ).
(e) Plot the time responses for \(x_{1}\) and \(x_{2}\) (in \(\mathrm{mm}\) ). Define the time vector as: \(t=0: 0.0001: 0.2\); (in seconds).

Ix k2 k x2 1m2 mi W