For the same system as described in problem 5, complete the following.
(a) The initial displacements for the system's free vibration are \(x_{1}(0)=0.378\) \(\mathrm{mm}\) and \(x_{2}(0)=1 \mathrm{~mm}\) and the initial velocities are \(\dot{x}_{1}(0)=0 \mathrm{~mm} / \mathrm{s}\) and \(\dot{x}_{2}(0)=0 \mathrm{~mm} / \mathrm{s}\). Plot the time responses for \(x_{1}\) and \(x_{2}\) (in \(\mathrm{mm}\) ). Define the time vector as: \(\mathrm{t}=0: 0.0001: 0.2\); (in seconds). What is the vibrating frequency for both \(x_{1}(t)\) and \(x_{2}(t)\) ? What is special about these initial conditions to give this result?
(b) The initial displacements for the system's free vibration are \(x_{1}(0)=\) \(-4.628 \mathrm{~mm}\) and \(x_{2}(0)=1 \mathrm{~mm}\) and the initial velocities are \(\dot{x}_{1}(0)=0 \mathrm{~mm} / \mathrm{s}\) and \(\dot{x}_{2}(0)=0 \mathrm{~mm} / \mathrm{s}\). Plot the time responses for \(x_{1}\) and \(x_{2}\) (in \(\left.\mathrm{mm}\right)\). Define the time vector as: \(\mathrm{t}=0: 0.0001: 0.2\); (in seconds). What is the vibrating frequency for both \(x_{1}(t)\) and \(x_{2}(t)\) ? What is special about these initial conditions to give this result?

Problem 5.

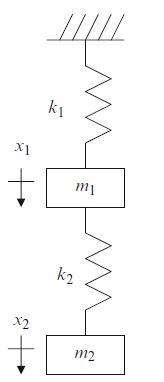
A two degree of freedom spring-mass system is displayed in Fig. P4.5. For harmonic free vibration, complete the following if \(k_{1}=2 \times 10^{6} \mathrm{~N} / \mathrm{m}\), \(m_{1}=0.8 \mathrm{~kg}, k_{2}=1 \times 10^{6} \mathrm{~N} / \mathrm{m}\), and \(m_{2}=1.4 \mathrm{~kg}\). The initial displacements for the system's free vibration are \(x_{1}(0)=2 \mathrm{~mm}\) and \(x_{2}(0)=1 \mathrm{~mm}\) and the initial velocities are \(\dot{x}_{1}(0)=0 \mathrm{~mm} / \mathrm{s}\) and \(\dot{x}_{2}(0)=5 \mathrm{~mm} / \mathrm{s}\).
• Calculate the two natural frequencies and mode shapes. Normalize the mode shapes (eigenvectors) to coordinate \(x_{2}\).
• Define the modal matrix and determine the modal mass and stiffness matrices.
• Write the uncoupled single degree of freedom time responses for the modal coordinates \(q_{1}\) and \(q_{2}\). Use the following form: \(q_{1,2}(t)=A_{1,2} \cos \left(\omega_{n_{1,2}} t\right)+\) \(B_{1,2} \sin \left(\omega_{n_{1,2}} t\right)\) with units of \(\mathrm{mm}\).

Ix k2 x2 1m2 k1 mi W