A two degree of freedom spring-mass-damper system is shown in Fig. P5.2. For harmonic forced vibration (due to the external force applied at coordinate \(x_{2}\) ), complete the following 

if \(k_{1}=8 \times 10^{7} \mathrm{~N} / \mathrm{m}, c_{1}=1000 \mathrm{~N}-\mathrm{s} / \mathrm{m}, m_{1}=50 \mathrm{~kg}\), \(k_{2}=5 \times 10^{7} \mathrm{~N} / \mathrm{m}, c_{2}=500 \mathrm{~N}-\mathrm{s} / \mathrm{m}\), and \(m_{2}=12 \mathrm{~kg}\).
(a) Show that proportional damping does not exist.
(b) Write a symbolic expression for the direct FRF \(X_{2} / F_{2}\) as a function of the frequency, \(\omega\), and mass, stiffness, and damping values, \(m_{1,2}, k_{1,2}\), and \(c_{1,2}\). Use the complex matrix inversion approach.

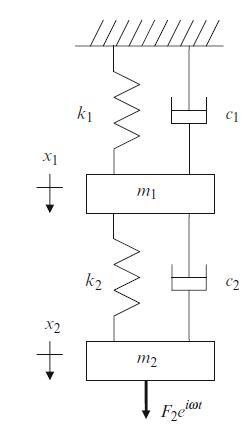
Fig. P5.2 Two degree of freedom spring-massdamper system under forced vibration.

(c) Write a symbolic expression for the cross FRF \(X_{1} / F_{2}\) as a function of the frequency, \(\omega\), and mass, stiffness, and damping values, \(m_{1,2}, k_{1,2}\), and \(c_{1,2}\). Use the complex matrix inversion approach.
(d) Plot the real and imaginary parts of the cross FRF, \(X_{1} / F_{2}\). Units should be \(\mathrm{m} / \mathrm{N}\) for the vertical axis and rad/s for the horizontal (frequency) axis. Use a frequency range of omega \(=0: 0.01: 3500 ;(\mathrm{rad} / \mathrm{s})\).

Transcribed Image Text:

ki x1 + mi X2 + k2 m2 3 02 Freicon