Consider the single degree of freedom spring-mass system shown in Fig. P5.3, where \(k=4 \times 10^{5} \mathrm{~N} / \mathrm{m}\) and \(m=8 \mathrm{~kg}\). It is being excited by a harmonic forcing function, \(F_{1} e^{i \omega_{f} t}\), at a frequency, \(\omega_{f}\).
(a) If the excitation frequency is \(200 \mathrm{rad} / \mathrm{s}\), design a dynamic absorber to eliminate the vibration at coordinate \(x_{1}\). The only available spring for use in the absorber is identical to the one already used in the system.

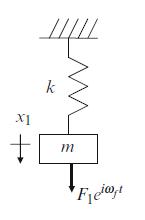
Fig. P5.3 Single degree of freedom system excited by the harmonic forcing function \(F_{1} e^{i \omega_{f} t}\)
(b) If the \(4 \times 10^{5} \mathrm{~N} / \mathrm{m}\) absorber spring is used in conjunction with a \(2 \mathrm{~kg}\) absorber mass, at what forced excitation frequency (in rad/s) will the steady-state vibration of coordinate \(x_{1}\) be eliminated?

Transcribed Image Text:

Ix k + m Fleit