A two degree of freedom spring-mass-damper system is shown Fig. P5.1. For harmonic forced vibration (due to the external force at coordinate \(x_{2}\) ), complete the following if \(k_{1}=2 \times 10^{5} \mathrm{~N} / \mathrm{m}, c_{1}=60 \mathrm{~N}-\mathrm{s} / \mathrm{m}, m_{1}=2.5 \mathrm{~kg}, k_{2}=5.5\) \(\times 10^{4} \mathrm{~N} / \mathrm{m}, c_{2}=16.5 \mathrm{~N}-\mathrm{s} / \mathrm{m}\), and \(m_{2}=1.2 \mathrm{~kg}\).

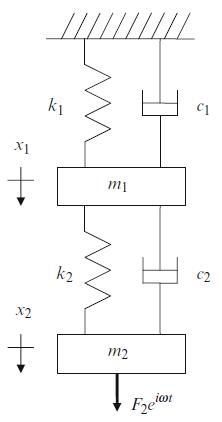
Fig. P5.1 Two degree of freedom spring-massdamper system under forced vibration

(a) Verify that proportional damping exists.
(b) Define the modal matrix and determine the modal mass, stiffness, and damping matrices. Note that the mode shapes should be normalized to the force location.
(c) Write expressions for the uncoupled single degree of freedom FRFs in modal coordinates, \(Q_{1} / R_{1}\) and \(Q_{2} / R_{2}\), and the direct FRF in local coordinates, \(X_{2} / F_{2}\).
(d) Plot the real and imaginary parts of the direct FRF, \(X_{2} / F_{2}\). Units should be \(\mathrm{m} / \mathrm{N}\) for the vertical axis and \(\mathrm{rad} / \mathrm{s}\) for the horizontal (frequency) axis. Use a frequency range of omega \(=0: 0.01: 500 ;(\mathrm{rad} / \mathrm{s})\).

Transcribed Image Text:

*+ /// k C1 X2 k2 mi m2 Freicot C2 3