Consider the system with (m_{2}=10 mathrm{~kg}) and (k_{2}=2000 mathrm{~N} / mathrm{m}). The right mass is displaced (10

Question:

Consider the system with \(m_{2}=10 \mathrm{~kg}\) and \(k_{2}=2000 \mathrm{~N} / \mathrm{m}\). The right mass is displaced \(10 \mathrm{~mm}\) from equilibrium while the left mass is held in place. The system is released from rest from this configuration.

(a) Determine the natural frequencies, mode shapes, and principal coordinates for the linearized system.

(b) Write the nonlinear differential equations governing the system using the principal coordinates of the linearized system as dependent variables.

Refer to the systems of Figure P12.32. The spring of stiffness \(k_{2}\) is a linear spring.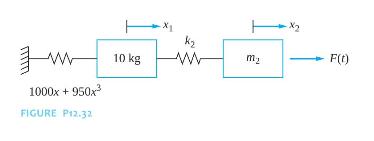
image text in transcribed