Determine the two lowest natural frequencies of the railroad bridge of Chapter Problem 7.84, if (k_{1}=5.5 times
Question:
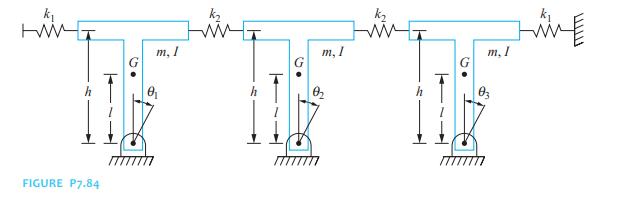
Determine the two lowest natural frequencies of the railroad bridge of Chapter Problem 7.84, if \(k_{1}=5.5 \times 10^{7} \mathrm{~N} / \mathrm{m}, k_{2}=1.2 \times 10^{7} \mathrm{~N} / \mathrm{m}, m=15,000 \mathrm{~kg}\), \(I=1.6 \times 10^{6} \mathrm{~kg} \cdot \mathrm{m}^{2}, l=6.7 \mathrm{~m}\), and \(h=8.8 \mathrm{~m}\).
Data From Chapter Problem 7.84:
A three degree-of-freedom model of a railroad bridge is shown in Figure P7.84. The bridge is composed of three rigid spans. Each span is pinned at its base. Using the angular displacements of the spans as generalized coordinates, derive the differential equations governing the motion of the bridge.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





