The equations for an armature-controlled dc motor are the following. The motor’s current is i and its rotational velocity is ω.

 

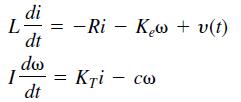
where L, R, and I are the motor’s inductance, resistance, and inertia; K_T and K_e are the torque constant and back emf constant; c is a viscous damping constant; and υ(t) is the applied voltage.

Use the values R = 0.8 /, L = 0.003 H, K_T = 0.05 N ∙ m/A, K_e = 0.05 V ∙ s/rad, c = 0, and I = 8 × 10^–5 kg ∙ m².

a. Suppose the applied voltage is 20 V. Plot the motor’s speed and current versus time. Choose a final time large enough to show the motor’s speed becoming constant.

b. Suppose the applied voltage is trapezoidal as given below.

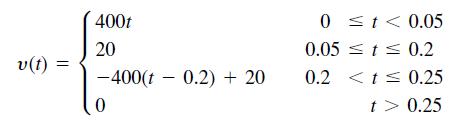
Plot the motor’s speed versus time for 0 ≤ t ≤ 0.3 s. Also plot the applied voltage versus time. How well does the motor speed follow a trapezoidal pro le?

Transcribed Image Text:

di L- dt - Ri – Kw + v(t) do Kri - | dt