A perfect matching is a matching in which every vertex is matched (Let G = (V, E) be an undirected bipartite graph with vertex partition V = L ? R, where |L| = |R|. For any X ? V, define the neighborhood of X as

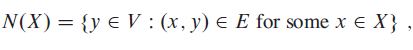
that is, the set of vertices adjacent to some member of X( Prove Hall?s theorem: there exists a perfect matching in G if and only if |A| ? |N(A)| for every subset A ? L.

Transcribed Image Text:

N(X)= {y e V : (x, y) E E for some x e X}