It is desired to predict the Darcy permeability k of a porous material that consists of many cylindrical fibers arranged in parallel. For simplicity, assume that long fibers of radius R are equally spaced and that the flow is parallel to their axes. A particularly symmetric configuration is shown in Fig. P7.6(a), in which the cross-section is divided into identical hexagonal cells. It is sufficient then to consider a single fiber. A further simplification is to approximate the hexagons of side length H as circles of radius λR, as enlarged in Fig. P7.6(b). For equal areas, λR = 0.91H.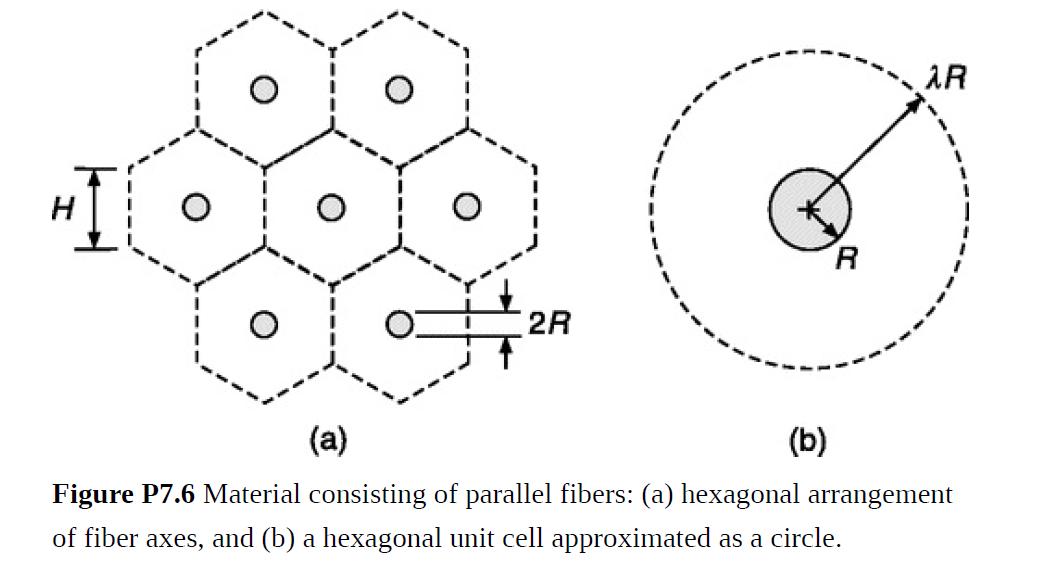

(a) Determine the fully developed velocity profile, vz(r), for a given pressure drop per unit length,

Based on the symmetry, you may assume that τ_rz = 0 at r = λR.

(b) Calculate the volume flow rate per fiber and use that to find the superficial velocity.

(c) If the fibers are widely spaced (λ ≫ 1), show that

where d(= 2R) is the fiber diameter and ϕ(= 1/λ²) is the volume fraction of fibers. Note that this result has the same form as Eq. (3.4-12), which is for randomly oriented fibers. The parallel arrangement and flow direction assumed here merely affected the constants (1⁄16 vs. 3⁄80 and 3⁄2 vs. 0.931).

Transcribed Image Text:

H 2R R λR (a) (b) Figure P7.6 Material consisting of parallel fibers: (a) hexagonal arrangement of fiber axes, and (b) a hexagonal unit cell approximated as a circle.