The objective is to predict how long it takes a small fluid sphere, initially at rest, to reach its terminal velocity. To derive the most general results for Re < 1, assume that the Hadamard–Rybczyński drag coefficient [Eq. (3.3-13)] is applicable. Results for solid spheres (or fluid spheres behaving as solids) may be obtained then by letting κ → ∞.

(a) Starting with the differential equation that governs the particle velocity, show that the time constant is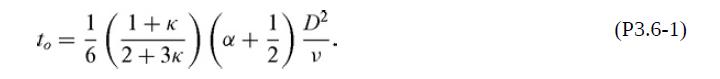

This is the same as that derived in Chisnell (1987) from detailed solutions for the pressure and velocity fields inside and outside a small fluid sphere. 

Show that it is also equivalent to Eq. (3.3-15).

(b) Using the notation of Example 3.3-3, show that the dimensionless velocity is

Given that e⁻³ = 0.05, this indicates that the velocity will reach 95% of its terminal value at τ = 3 or t = 3t_o.

Transcribed Image Text:

1 1+K ²0 = ² ( ₁ + x ) ( ~ + ² ) ² ² ² to +3K 2 (P3.6-1)