Two mechanisms for the deposition of inhaled particles in the airways are gravitational settling, discussed in Section 3.3, and inertial impaction, depicted in Fig. P3.7. If fluid paths suddenly curve, as when an airway bifurcates, relatively large particles tend to continue along straight lines and may collide with a wall. It is desired to compare the rates of gravitational settling and inertial impaction at various locations within the respiratory tract.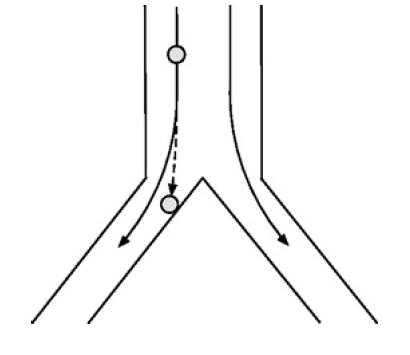

(a) The measure of particle inertia is the stopping distance D_s, which is how far a particle drifts when its propelling force is removed. For simplicity, suppose that a particle is being carried initially at a velocity u(0) = u_o in the x direction, and then the fluid suddenly makes a 90° turn. Because there is no longer an x component of the fluid velocity, drag gradually reduces u(t) to zero. This can be modeled by setting g = 0 in Eq. (3.3-16). Show that, for a particle with a diameter d and u_od/ν < 1,

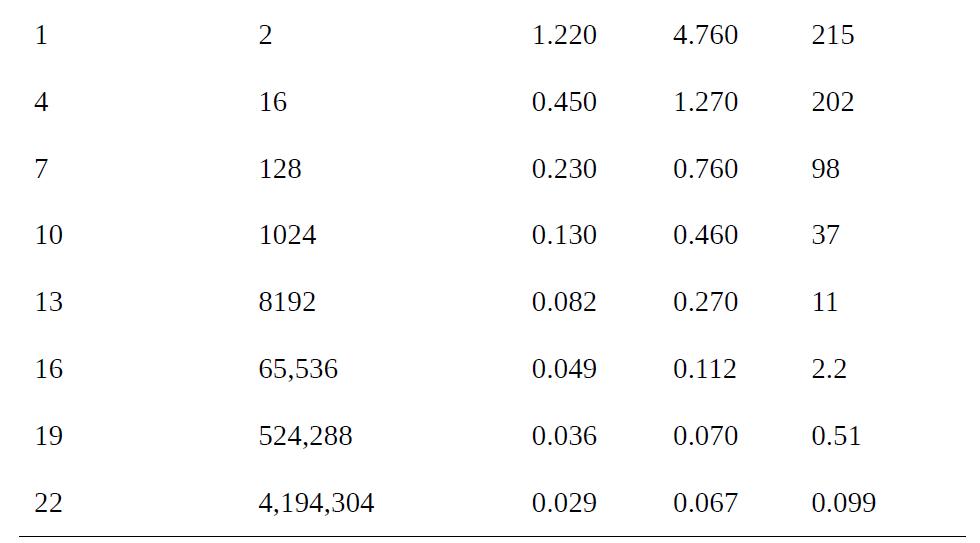
(b) There are millions of airway segments, from the trachea to tiny alveoli deep in the lungs. According to a standard anatomical model, human airways bifurcate 23 times, ultimately generating 8.39 × 10⁶ branches. The diameter (D), length (L), and air velocity (U) at selected locations are given in Table P3.7. An order-of-magnitude estimate of the probability of inertial impaction within a given segment is p_i ∼ D_s/D. Calculate D_s/D as a function of d and location. If a therapeutic aerosol needs to reach far into the lungs, explain why one with d = 1 μm or 10 μm will be much more effective than one with d = 100 μm. A typical particle density is ρ_o = 1000 kg/m³, and μ = 1.90 × 10⁻⁵ Pa s and ρ = 1.11 kg/m³ for humid air at body temperature (37 °C).

(c) The probability of gravitational deposition is roughly the settling distance divided by D, or p_s ∼ u_sL/(UD), where u_s is the Stokes terminal velocity. Because D_s and u_s both vary as d², the relative importance of the two mechanisms is independent of particle size (within the Stokes range). However, it depends very much on location. Show that p_i/p_s ∼ U²/(gL) = Fr (a Froude number) and plot Fr as a function of the generation number. Where in the respiratory network is inertial impaction more important and where is gravitational settling more important?