With reference to Ex. 10.4 (a) Apply Eq. (10.7) to Eq. (A) to verify Eqs. (B) and
Question:
With reference to Ex. 10.4
(a) Apply Eq. (10.7) to Eq. (A) to verify Eqs. (B) and (C).
(b) Show that Eqs. (B) and (C) combine in accord with Eq. (10.11) to regenerate Eq. (A).
Eq. (10.11)
![]()
(c) Show that Eqs. (B) and (C) satisfy Eq. (10.14), the Gibbs/Duhem equation.
(d) Show that at constant T and P,
(dH̅1/ dx1) x1=1 = (dH̅2/ dx1) x1=0 = 0
(e) Plot values of H, H̅1 , and H̅2 , calculated by Eqs. (A), (B), and (C), vs. x1. Label points H1, H2, H̅∞1 , and H̅∞2 , and show their values.
Ex. 10.4
The enthalpy of a binary liquid system of species 1 and 2 at fixed T and P is represented by the equation:
H = 400x1 + 600x2 + x1 x2 (40x1 + 20x2)
where H is in J·mol–1. Determine expressions for H̅1 and H̅2 as functions of x1, numerical values for the pure-species enthalpies H1 and H2, and numerical values for the partial enthalpies at infinite dilution H̅∞1 and H̅∞2.
Eq. (10.7)

(A) & (B) Eq. (10.7) & (10.11) (A) (B) (C)
Eq. (10.7). For binary systems, however, an alternative procedure may be more convenient. Written for a binary solution, the summability relation, Eq. (10.11), becomes:
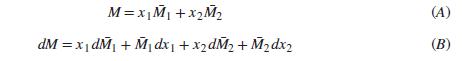
![]()
(c) Eq. (10.14) (B) & (C)
When M is known as a function of x1 at constant T and P, the appropriate form of the Gibbs/ Duhem equation is Eq. (10.14), expressed here as:
![]()
![]()
Step by Step Answer:

Introduction To Chemical Engineering Thermodynamics
ISBN: 9781259696527
8th Edition
Authors: J.M. Smith, Hendrick Van Ness, Michael Abbott, Mark Swihart





