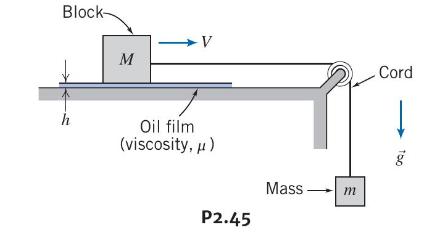
A block of mass \(M\) slides on a thin film of oil. The film thickness is \(h\) and the area of the block is \(A\). When released, mass \(m\) exerts tension on the cord, causing the block to accelerate. Neglect friction in the pulley and air resistance. Develop an algebraic expression for the viscous force that acts on the block when it moves at speed \(V\). Derive a differential equation for the block speed as a function of time. Obtain an expression for the block speed as a function of time. The mass \(M=5 \mathrm{~kg}, m=1 \mathrm{~kg}, A=25 \mathrm{~cm}^{2}\), and \(h=0.5 \mathrm{~mm}\). If it takes \(1 \mathrm{~s}\) for the speed to reach \(1 \mathrm{~m} / \mathrm{s}\), find the oil viscosity \(\mu\). Plot the curve for \(V(t)\).

Transcribed Image Text:

Block- M V Cord h Oil film (viscosity, ) P2.45 Mass m 100