An engineer is measuring a quantity . It is assumed that there is a random error in

An engineer is measuring a quantity θ. It is assumed that there is a random error in each measurement, so the engineer will take n measurements and report the average of the measurements as the estimated value of θ. Here, n is assumed to be large enough so that the central limit theorem applies. If X_i is the value that is obtained in the ith measurement, we assume that X_i = θ +W_i, where Wi is the error in the ith measurement. We assume that the Wi's are i. i. d. with EW_i = 0 and Var(W_i) = 4 units. The engineer reports the average of the measurements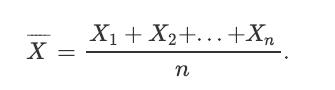

How many measurements does the engineer need to make until he is 90% sure that the final error is less than 0.25 units? In other words, what should the value of n be such that

Transcribed Image Text:

X X₁ + X₂+...+Xn n