Consider a continuous Markov chain with two states S = {0, 1}. Assume the holding time parameters
Question:
Consider a continuous Markov chain with two states S = {0, 1}. Assume the holding time parameters are given by λ0 = λ1 = λ > 0. That is, the time that the chain spends in each state before going to the other state has an Exponential(λ) distribution.
a. Draw the state diagram of the embedded (jump) chain.
b. Find the transition matrix P(t). You might want to use the following identities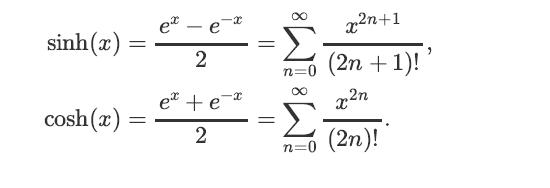
Transcribed Image Text:
sinh(2) cosh (x) = = et - e 2 e +ex 2 = = x²n+1 n=0 (2n +1)!' 2n x n=0 (2n)!
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Answer rating: 45% (11 reviews)
a There are two states in the chain and none of them are absorbing since 0 Since we do not allow sel...View the full answer

Answered By

Ashington Waweru
I am a lecturer, research writer and also a qualified financial analyst and accountant. I am qualified and articulate in many disciplines including English, Accounting, Finance, Quantitative spreadsheet analysis, Economics, and Statistics. I am an expert with sixteen years of experience in online industry-related work. I have a master's in business administration and a bachelor’s degree in education, accounting, and economics options.
I am a writer and proofreading expert with sixteen years of experience in online writing, proofreading, and text editing. I have vast knowledge and experience in writing techniques and styles such as APA, ASA, MLA, Chicago, Turabian, IEEE, and many others.
I am also an online blogger and research writer with sixteen years of writing and proofreading articles and reports. I have written many scripts and articles for blogs, and I also specialize in search engine
I have sixteen years of experience in Excel data entry, Excel data analysis, R-studio quantitative analysis, SPSS quantitative analysis, research writing, and proofreading articles and reports. I will deliver the highest quality online and offline Excel, R, SPSS, and other spreadsheet solutions within your operational deadlines. I have also compiled many original Excel quantitative and text spreadsheets which solve client’s problems in my research writing career.
I have extensive enterprise resource planning accounting, financial modeling, financial reporting, and company analysis: customer relationship management, enterprise resource planning, financial accounting projects, and corporate finance.
I am articulate in psychology, engineering, nursing, counseling, project management, accounting, finance, quantitative spreadsheet analysis, statistical and economic analysis, among many other industry fields and academic disciplines. I work to solve problems and provide accurate and credible solutions and research reports in all industries in the global economy.
I have taught and conducted masters and Ph.D. thesis research for specialists in Quantitative finance, Financial Accounting, Actuarial science, Macroeconomics, Microeconomics, Risk Management, Managerial Economics, Engineering Economics, Financial economics, Taxation and many other disciplines including water engineering, psychology, e-commerce, mechanical engineering, leadership and many others.
I have developed many courses on online websites like Teachable and Thinkific. I also developed an accounting reporting automation software project for Utafiti sacco located at ILRI Uthiru Kenya when I was working there in year 2001.
I am a mature, self-motivated worker who delivers high-quality, on-time reports which solve client’s problems accurately.
I have written many academic and professional industry research papers and tutored many clients from college to university undergraduate, master's and Ph.D. students, and corporate professionals. I anticipate your hiring me.
I know I will deliver the highest quality work you will find anywhere to award me your project work. Please note that I am looking for a long-term work relationship with you. I look forward to you delivering the best service to you.
3.00+
2+ Reviews
10+ Question Solved
Related Book For 

Introduction To Probability Statistics And Random Processes
ISBN: 9780990637202
1st Edition
Authors: Hossein Pishro-Nik
Question Posted:
Students also viewed these Business questions
-
Consider the continuous Markov chain of Example 11.17: A chain with two states S = {0, 1} and 0 = 1 = > 0. In that example, we found that the transition matrix for any t 0 is given by Find the...
-
Consider the co ntinuous Markov chain of Example 11.17: A chain with two states S = {0, 1} and 0 = 1 = > 0. In that example, we found that the transition matrix for any t 0 is given by a. Find...
-
The generator matrix for the continuous Markov chain of Example 11.17 is given by Find the stationary distribution for this chain by solving G = 0. Example 11.17 Consider a continuous Markov chain...
-
Write out the equation for the following chemical reaction and balance it. Solid potassium chlorate, KCIO3, decomposes to form solid potassium chloride and diatomic oxygen gas. What is the...
-
What is an equivalent unit of production, and why is it a necessary concept to employ in a process costing system?
-
Consider the following decision table, which Joe Blackburn has developed for Vanderbilt Enterprises: Which decision alternative maximizes the expected value of thepayoff? STATES OF NATURE MEDIUM S100...
-
The following is true of high-prototypical objects: (a) They have high family resemblance; (b) statements about them are verified rapidly; (c) they are named first; and (d) they are affected more by...
-
Calvin Jacobs is a widower who recently retired after a long career with a major Midwestern manufacturer. Beginning as a skilled craftsman, he worked his way up to the level of shop supervisor over a...
-
A Data Warehouse/Date Mining solution would be appropriate for the following use case for a national retailer: log Understanding the impact of multiple assortment plans across fifteen geographical...
-
Consider the Markov chain shown in Figure 11.15. Assume that 0 < p < 1/2. Does this chain have a limiting distribution?
-
Consider the Markov chain of Problem 16. Again assume X 0 = 4. We would like to find the expected time (number of steps) until the chain gets absorbed in R 1 or R 2 . More specifically, let T be the...
-
Design an op-amp summer to produce the output voltage \(v_{O}=2 v_{I 1}-\) \(10 v_{I 2}+3 v_{I 3}-v_{I 4}\). Assume the largest resistor value is \(500 \mathrm{k} \Omega\), and the input impedance...
-
Dynamic capability is the ability for change and manage corporate learning. It allows an enterprise to adapt, develop and respond to future opportunities and discontinuous technologies. Innovation...
-
What potential solutions can organizations try to help support the adoption of a CDSS? In other words, what are some ways an organization can address the factors of implementation obstruction that...
-
Identify and briefly describe and discuss the three most important factors in building and maintaining trust among virtual global team members. Include in your discussion how you can leverage these...
-
Management is what tradition used to call a liberal art: "liberal" because it deals with the fundamentals of knowledge, self-knowledge, wisdom, and leadership; "art" because it is a practice and...
-
Draft a five hundred and twenty five- to seven hundred-word internal communication planthat appropriately details your proposed solution to the internal team at CVS PHARMACY. In your communication...
-
Discuss the benefits and drawbacks of the following methods of forecasting: a. Jury of executive opinion b. The Delphi method c. Opinion polls Each method has its uses. What are they?
-
Nate prepares slides for his microscope. In 1 day he prepared 12 different slides. Which equation best represents y, the total number of slides Nate prepares in x days if he continues at this rate? A...
-
Sally owns a small C corporation that has provided health insurance coverage for Sally and the companys three other employees. The insurance coverage for Sally and the three employees is individual...
-
Maria was planning to paint the interior of her apartment over a three-day weekend. Her employer asked her to work all three days and will pay her $600 overtime. She called a professional painter who...
-
Able Corporation is a closely held company engaged in the manufacture and retail sales of automotive parts. Able maintains a qualified pension plan for its employees but has not offered nontaxable...
-
Following is a series of independent cases . In each situation, indicate the cash distribution to be made to partners at the end of the liquidation process. Unless otherwise stated, assume that all...
-
ASSETS LIABILITES AND EQUITY TII TTI TIT TTT EXPENSES REVENUES Inceresumman T T
-
. In explain the problem Distinguish between a meteor, a meteoroid, a meteorite, an asteroid, and a comet

Study smarter with the SolutionInn App


