For three or more events which are not independent, the probability that they will all occur is obtained by multiplying the probability that one of the events will occur, times the probability that a second of the events will occur given that the first event has occurred, times the probability that a third of the events will occur given that the first two events have occurred, and so on. For instance, for three events we can write

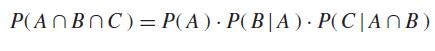
and we find that the probability of drawing without replacement three aces in a row from an ordinary deck of 52 playing cards is

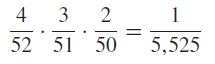
(a) If six bullets, of which three are blanks, are randomly inserted into a gun, what is the probability that the first three bullets fired will all be blanks?

(b) In a certain city during the month of May, the probability that a rainy day will be followed by another rainy day is 0.80 and the probability that a sunny day will be followed by a rainy day is 0.60.
Assuming that each day is classified as being either rainy or sunny and that the weather on any given day depends only on the weather the day before, find the probability that in the given city a rainy day in May is followed by two more rainy days, then a sunny day, and finally another rainy day.

(c) A department store which bills its charge-account customers once a month has found that if a customer pays promptly one month, the probability is 0.90 that he will also pay promptly the next month; however, if a customer does not pay promptly one month, the probability that he will pay promptly the next month is only 0.50. What is the probability that a customer who has paid promptly one month will not pay promptly the next three months?

(d) If 5 of a company’s 12 delivery trucks do not meet emission standards and 4 of the 12 trucks are randomly picked for inspection, what is the probability that none of them meets emission standards?

Transcribed Image Text:

P(ANBOC) = P(A) P(B|A). P(C|ANB)