Suppose X1, . . . , Xn constitute a sample from a uniform distribution on (0, ), where is unknown. Their joint density is

Suppose X1, . . . , Xn constitute a sample from a uniform distribution on (0, θ), where θ is unknown. Their joint density is thus

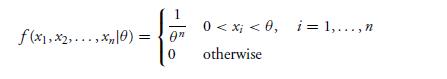
This density is maximized by choosing θ as small as possible. Since θ must be at least as large as all of the observed values xi , it follows that the smallest possible choice of θ is equal to max(x1, x2, . . . , xn). Hence, the maximum likelihood estimator of θ is

It easily follows from the foregoing that the maximum likelihood estimator of θ/2, the mean of the distribution, is max(X1, X2, . . . , Xn)/2.

f(x1,x2x0): == 0 0 < x