A free particle of mass m is confined to a ring of circumference L such that Ψ (x+L) = Ψ (x). The unperturbed Hamiltonian is

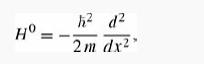
to which we add a perturbation

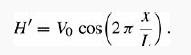
(a) Show that the unperturbed states may be written

for n = 0, ±1, ±2 and that, apart from n = 0, all of these states are two-fold degenerate.
(b) Find a general expression for the matrix elements of the perturbation:

(c) Consider the degenerate pair of states with n = ±1. Construct the matrix W and calculate the first-order energy corrections, E¹. Note that the degeneracy does not lift at first order. Therefore, diagonalizing W does not tell us what the “good” states are.
(d) Construct the matrix  W² (Problem 7.40) for the states n = ±1, and show that the degeneracy lifts at second order. What are the good linear combinations of the states with n = ±1?
(e) What are the energies, accurate to second order, for these states?

Transcribed Image Text:

НО h² d2 2m dx2