If it happens that the square root in Equation 7.33 vanishes, then E 1 + = E
Question:
If it happens that the square root in Equation 7.33 vanishes, then E1+ = E1-; the degeneracy is not lifted at first order. In this case, diagonalizing the W matrix puts no restriction on α and β and you still don’t know what the “good” states are. If you need to determine the “good” states— for example to calculate higher-order corrections—you need to use second-order degenerate perturbation theory.
(a) Show that, for the two-fold degeneracy studied in Section 7.2.1, the first-order correction to the wave function in degenerate perturbation theory is
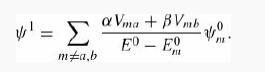
(b) Consider the terms of order λ2 (corresponding to Equation 7.8 in the nondegenerate case) to show that α and β are determined by finding the eigenvectors of the matrix W2 (the superscript denotes second order, not W squared) where
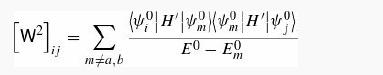
and that the eigenvalues of this matrix correspond to the second-order energies E2.
(c) Show that second-order degenerate perturbation theory, developed in (b), gives the correct energies to second order for the three-state Hamiltonian in Problem 7.39.

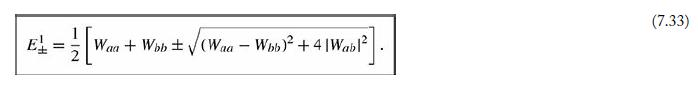
Step by Step Answer:

Introduction To Quantum Mechanics
ISBN: 9781107189638
3rd Edition
Authors: David J. Griffiths, Darrell F. Schroeter





