Consider a particle of mass m moving in a potential V(x) with period a. We know from Bloch’s theorem that the wave function can be written in the form of Equation 6.12.

(a) Show that u satisfies the equation

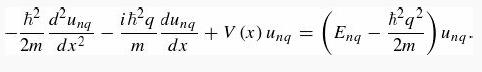
(b) Use the technique from Problem 2.61 to solve the differential (6.14) equation for u_nq. You need to use a two-sided difference for the first derivative so that you have a Hermitian matrix to diagonalize:

For the potential in the interval 0 to a let

with V₀ = 20ћ²/2ma². (You will need to modify the technique slightly to account for the fact that the function u_nq is periodic.) Find the lowest two energies for the following values of the crystal momentum: qa = -π,-π/2, 0, π/2, π. q and q+2π/a describe the same wave function (Equation 6.12), so there is no reason to consider values of  qa outside of the interval from -π to π. In solid state physics, the values of q inside this range constitute the first Brillouin zone.
(c) Make a plot of the energies E_1q and E_2q for values of q between -π/a and π/a. If you’ve automated the code that you used in part (b), you should be able to show a large number of q values in this range. If not, simply plot the values that you computed in (b).

Transcribed Image Text:

ħ² d²ung 2m dx² iħ²q dung dx m + V (x) Ung = Eng - ħi²q² 2m Ung-