For the harmonic oscillator [V(x) = (1/2)kx 2 ], the allowed energies are where = k/m is the classical frequency. Now suppose the spring

For the harmonic oscillator [V(x) = (1/2)kx²], the allowed energies are

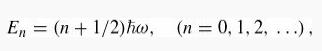
where ω = √k/m is the classical frequency. Now suppose the spring constant increases slightly: k→ (1+∈)k. (Perhaps we cool the spring, so it becomes less flexible.)
(a) Find the exact new energies (trivial, in this case). Expand your formula as a power series in ϵ, up to second order.
(b) Now calculate the first-order perturbation in the energy, using Equation 7.9. What is H' here? Compare your result with part (a).

En = (n + 1/2)w, (n = 0, 1, 2, ...),