One way to obtain the allowed energies of a potential well numerically is to turn the Schrdinger

One way to obtain the allowed energies of a potential well numerically is to turn the Schrödinger equation into a matrix equation, by discretizing the variable x. Slice the relevant interval at evenly spaced points, {x_j} with x_j+1 - x_j Ξ Δx, and let Ψ_j Ξ Ψ (x_j) (likewise V_j Ξ V (x_j)). then

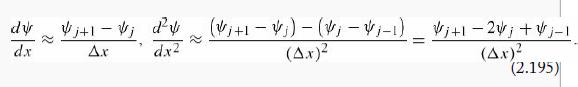
(The approximation presumably improves as  Δx decreases.) The discretized Schrödinger equation reads

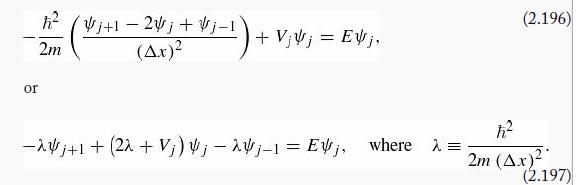
In matrix form,

HΨ = EΨ

where (letter v_j Ξ V_j/λ)

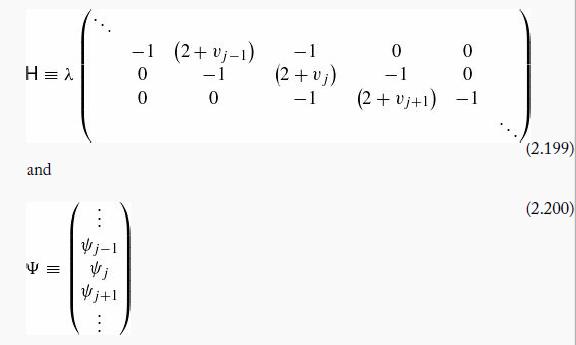
(what goes in the upper left and lower right corners of H depends on the boundary conditions, as we shall see). Evidently the allowed energies are the
eigenvalues of the matrix H (or would be, in the limit  Δx → 0). Apply this method to the infinite square well. Chop the interval (0 ≤ x ≤ α) into N+1 equal segments (so that Δx = α/(N+1)), letting x₀ Ξ 0 and x_N+1 Ξ α. The boundary conditions fix Ψ₀ = Ψ_N+1 = 0, leaving

(a) Construct the N x N matrix H, for N =1, N = 2 and N = 3. (Make sure you are correctly representing Equation 2.197 for the special cases j =1 and j = N.)
(b) Find the eigenvalues of H for these three cases “by hand,” and compare them with the exact allowed energies (Equation 2.30).

(c) Using a computer (Mathematica’s Eigenvalues package will do it) find the five lowest eigenvalues numerically for N = 10 and N = 100, and compare the exact energies.
(d) Plot (by hand) the eigenvectors for N = 1, 2, and 3, and (by computer, Eigenvectors) the first three eigenvectors for N = 10 and N = 100.

Transcribed Image Text:

dx Vj+1 -₁ ² (₁+1 − ₁) − (−₁−₁) - A.x dx² (4.x)² = Vj+1-2; +j-1 (4x)² (2.195)