Suppose where is some positive constant with the appropriate dimensions. Wed like to find the bound

Suppose

where α is some positive constant with the appropriate dimensions. We’d like to find the bound states—solutions to the time-independent Schrödinger equation

with negative energy (E < 0).
(a) Let’s first go for the ground state energy, E₀. Prove, on dimensional grounds, that there is no possible formula for E₀ —no way to construct (from the available constants m, ћ, and α) a quantity with the units of energy. That’s weird, but it gets worse ….
(b) For convenience, rewrite Equation 2.190 as

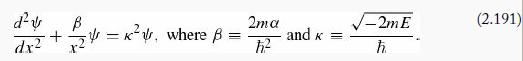
Show that if Ψ (x) satisfies this equation with energy E, then so too does Ψ (λ,x), with energy E' = λ²E, for any positive number λ. [This is a catastrophe: if there exists any solution at all, then there’s a solution for every (negative) energy! Unlike the square well, the harmonic oscillator, and every other potential well we have encountered, there are no discrete allowed states—and no ground state. A system with no ground state—no lowest allowed energy—would be wildly unstable, cascading down to lower and lower levels, giving off an unlimited amount of energy as it falls. It might solve our energy problem, but we’d all be fried in the process.] Well, perhaps there simply are no solutions at all ….
(c) (Use a computer for the remainder of this problem.) Show that

satisfies Equation 2.191 (here K_ig is the modified Bessel function of order ig, and Plot this function, for g = 4 (you might as well let k = 1 for the graph; this just sets the scale of length). Notice that it goes to 0 as x → 0 and as And it’s normalizable:determine A. How about the old rule that the number of nodes counts the number of lower-energy states? This function has an infinite number of nodes, regardless of the energy (i.e. of k). I guess that’s consistent, since for any E there are always an infinite number of states with even lower energy.
(d) This potential confounds practically everything we have come to expect. The problem is that it blows up too violently as x → 0. If you move the “brick wall” over a hair,

it’s suddenly perfectly normal. Plot the ground state wave function, for g = 4 and ε = 1 (you’ll first need to determine the appropriate value of k), from x = 0 to x = 6. Notice that we have introduced a new parameter (ε), with the dimensions of length, so the argument in (a) is out the window. Show that the ground state energy takes the form

for some function f of the dimensionless quantity β.

Transcribed Image Text:

V (x) = x > 0. x ≤ 0. (2.189)