Performing a variational calculation requires finding the minimum of the energy, as a function of the variational parameters. This is, in general, a very hard problem. However, if we choose the form of our trial wave function judiciously, we can develop an efficient algorithm. In particular, suppose we use a linear combination of functions ∅_n (x):

where the C_n are the variational parameters. If the ∅_n are an orthonormal set ((∅_m|∅_n) = δ_mn), but Ψ(x) is not necessarily normalized, then (H) is

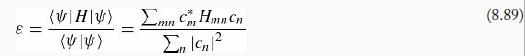
where H_mn = (Φ_m|H|Φ_n) . Taking the derivative with respect to c* j (and setting the result equal to 0) gives

recognizable as the jth row in an eigenvalue problem:

The smallest eigenvalue of this matrix H gives a bound on the ground state energy and the corresponding eigenvector determines the best variational wave function of the form 8.88.
(a) Verify Equation 8.90.
(b) Now take the derivative of Equation 8.89 with respect to c j and show that you get a result redundant with Equation 8.90.
(c) Consider a particle in an infinite square well of width a, with a sloping floor:

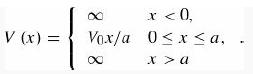
Using a linear combination of the first ten stationary states of the infinite square well as the basis functions,

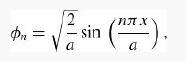
determine a bound for the ground state energy in the case V₀ = 100ћ²/ma². Make a plot of the optimized variational wave function.

N + (x) = (x), n=l (8.88)