Use separation of variables in cartesian coordinates to solve the infinite cubical well (or “particle in a box”):

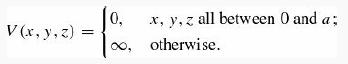
(a) Find the stationary states, and the corresponding energies.
(b) Call the distinct energies E₁,E₂,E₃, ...., in order of increasing energy. Find E₁,E₂,E₃,E₄,E₅, and E₆. Determine their degeneracies (that is, the number of different states that share the same energy).  In one dimension degenerate bound states do not occur (see Problem 2.44), but in three dimensions they are very common.
(c) What is the degeneracy of E₁₄, and why is this case interesting?

Problem 2.44

If two (or more) distinct solutions to the (time-independent) Schrödinger equation have the same energy E, these states are said to be degenerate. For example, the free particle states are doubly degenerate—one solution representing motion to the right, and the other motion to the left. But we have never encountered normalizable degenerate solutions, and this is no accident. Prove the following theorem: In one dimension (-∞ < x < ∞) there are no degenerate bound states.

Transcribed Image Text:

V(x, y, z) 0, 100, x, y, z all between 0 and a; otherwise.