In the context of the proof of Theorem 10.12, prove that (Lambda_{n}=nleft(hat{theta}_{n}-ight.) (left.theta_{0}ight)^{2} Ileft(theta_{0}ight)+o_{p}left(n^{-1}ight)), as (n ightarrow
Question:
In the context of the proof of Theorem 10.12, prove that \(\Lambda_{n}=n\left(\hat{\theta}_{n}-ight.\) \(\left.\theta_{0}ight)^{2} I\left(\theta_{0}ight)+o_{p}\left(n^{-1}ight)\), as \(n ightarrow \infty\) where \(\theta_{1, n}=\theta_{0}+n^{-1 / 2} \delta\).
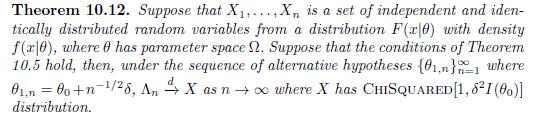
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





