Let (X_{1}, ldots, X_{n}) be a set of independent and identically distributed random variables from a distribution
Question:
Let \(X_{1}, \ldots, X_{n}\) be a set of independent and identically distributed random variables from a distribution \(F\) with variance \(\mu_{2}\) where \(E\left(\left|X_{1}ight|^{4}ight)
a. Prove that the sample variance can be rewritten as
\[S_{n}^{2}=\frac{1}{2 n(n-1)} \sum_{i=1}^{n} \sum_{j=1}^{n}\left(X_{i}-X_{j}ight)^{2}\]
b. Prove that \(S_{n}^{2}\) is an unbiased estimator of \(\mu_{2}\), that is, prove that \(E\left(S_{n}^{2}ight)=\) \(\mu_{2}\) for all \(\mu_{2}>0\).
c. Prove that the variance of \(\hat{\mu}_{2}\) is
\[V\left(\hat{\mu}_{2}ight)=n^{-1}\left(\mu_{4}-\frac{n-3}{n-1} \mu_{2}^{2}ight) .\]
d. Use the results derived above to prove that \(\hat{\mu}_{2}\) is a consistent estimator of \(\mu_{2}\). That is, prove that \(\hat{\mu}_{2} \xrightarrow{p} \mu_{2}\) as \(n ightarrow \infty\).
e. Relate the results observed here with the results given in Theorem 3.21.
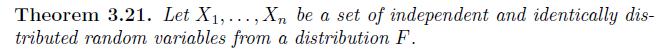
Step by Step Answer:






