Prove Theorem 6.4. That is, suppose that (left{X_{n}ight}_{n=1}^{infty}) be a sequence of random variables such that (sigma_{n}^{-1}left(X_{n}-muight)
Question:
Prove Theorem 6.4. That is, suppose that \(\left\{X_{n}ight\}_{n=1}^{\infty}\) be a sequence of random variables such that \(\sigma_{n}^{-1}\left(X_{n}-\muight) \xrightarrow{d} Z\) as \(n ightarrow \infty\) where \(Z\) is a \(\mathrm{N}(0,1)\) random variable and \(\left\{\sigma_{n}ight\}_{n=1}^{\infty}\) is a real sequence such that
\[\lim _{n ightarrow \infty} \sigma_{n}=0\]
Let \(g\) be a real function such that \[\left.\frac{d^{m}}{d x^{m}} g(x)ight|_{x=\mu} eq 0\]
for some \(m \in \mathbb{N}\) where \[\left.\frac{d^{k}}{d x^{k}} g(x)ight|_{x=\mu}=0\]
for all \(k \in\{1, \ldots, m-1\}\). Then prove that \[\frac{m !\left[g\left(X_{n}ight)-g(\mu)ight]}{\sigma_{n}^{m} g^{\prime}(\mu)} \xrightarrow{d} Z^{m}\]
as \(n ightarrow \infty\).
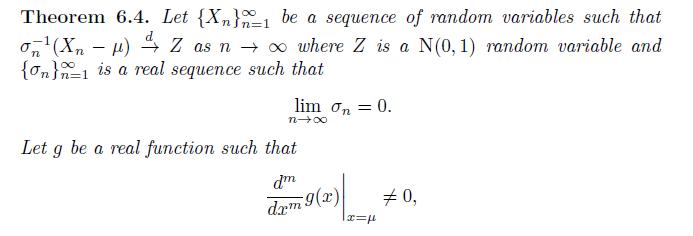
Step by Step Answer:






