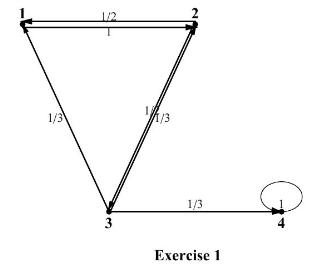
Consider the Markov chain with the transition diagram below. Suppose that there are two possible actions, labelled 0 and 1 . Under action 0 , the chain moves according to this transition diagram, and under action 1 , the chain moves with certainty to state 2 . Let \(\mathbf{u}\) be the stationary policy with action function defined by:

\[ u(i)= \begin{cases}0 & \text { if } i=1,2 \\ 1 & \text { if } i=3,4\end{cases} \]

If, for a certain experimental outcome \(\omega\), we observe \(X_{0}(\omega)=1\), \(X_{2}(\omega)=3, X_{3}(\omega)=2\), what are the first four actions taken under this policy? Again for this outcome, if the reward function is \(r(i, a)=i-a\), what are the first four rewards?

Transcribed Image Text:

1/2 1/3 1113 1/3 3 1/3 Exercise 1 G