Consider the problem: (a) Sketch the feasible region, find the coordinates of the corner points, and find
Question:
Consider the problem:
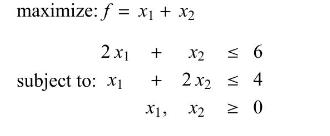
(a) Sketch the feasible region, find the coordinates of the corner points, and find the optimal value.
(b) Repeat
(a) if the right-hand side constants are changed to \(6+h_{1}\) and \(4+h_{2}\), respectively. Under what conditions on \(h_{1}\) and \(h_{2}\) are \(x_{1}\) and \(x_{2}\) still basic in the optimal solution?
(c) Perform the simplex algorithm on the problem in part (b), noting the connection between the conditions on \(h_{1}\) and \(h_{2}\) derived there, and the choice of entering basic variables.
Exercises (14)-(16) step the reader through a proof of the simplex algorithm. In these problems, we suppose that we begin with a standard maximum problem (1)-(2) whose constraints have been turned into equality constraints by the introduction of slack variables. Refer to the statement of the simplex algorithm. We amend step 2 in the following way: include into the entrance condition for loop 3 a check for a non-basic variable column with all non-negative coefficients. If this condition causes loop termination, then in place of step 4, return a message that the problem is unbounded.
Step by Step Answer:

Introduction To The Mathematics Of Operations Research With Mathematica
ISBN: 9781574446128
1st Edition
Authors: Kevin J Hastings





