Consider the following expenditure share equation where the budget share for food WFOOD is expressed as a function of total expenditure TOTEXP.

In Exercise 4.12, it was noted that the elasticity of expenditure on food with respect to total expenditure is given by

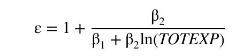
Also, in Exercise 5.18 it was indicated that a good is a necessity if \(\beta_{2}

a. Show that \(\beta_{2}

b. Use observations in the data file london5 to estimate (XR5.19.1) and comment on the results.

c. Find point estimates and \(95 \%\) interval estimates for the mean budget share for food, for total expenditure values (i) TOTEXP \(=50\) (the fifth percentile of TOTEXP), (ii) TOTEXP \(=90\) (the median), and (iii) TOTEXP \(=170\) (the 95th percentile).

d. Find point estimates and \(95 \%\) interval estimates for the elasticity \(\varepsilon\), for total expenditure values (i) TOTEXP \(=50\) (the fifth percentile), (ii) TOTEXP \(=90\) (the median), and (iii) TOTEXP \(=170\) (the 95th percentile).

e. Comment on how the mean budget share and the expenditure elasticity for food change as total expenditure changes. How does the reliability of estimation change as total expenditure changes?

Data From Exercise 5.18:-

Consider the following two expenditure share equations where the budget share for food WFOOD, and the budget share for clothing WCLOTH, are expressed as functions of total expenditure TOTEXP.

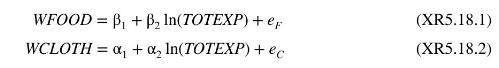
a. A commodity is regarded as a luxury if the coefficient of \(\ln (T O T E X P)\) is positive and a necessity if it is negative. What signs would you expect for \(\beta_{2}\) and \(\alpha_{2}\) ?

b. Using the data in the file london5, estimate the above equations using observations on households with one child. Comment on the estimates and their significance. Can you explain any possibly counterintuitive outcomes?

c. Using a \(1 \%\) significance level, test \(H_{0}: \beta_{2} \geq 0\) against the alternative \(H_{1}: \beta_{2}

d. Using a \(1 \%\) significance level, test \(H_{0}: \alpha_{2} \geq 0\) against the alternative \(H_{1}: \alpha_{2}

e. Estimate the two equations using observations on households with two children. Construct \(95 \%\) interval estimates for \(\beta_{2}\) and \(\alpha_{2}\) for both one- and two-child households. Based on these interval estimates, would you conjecture that the coefficients of \(\ln (T O T E X P)\) are the same or different for one- and two-child households.

f. Use all observations to estimate the following two equations and test, at a \(95 \%\) significance level, whether your conjectures in part (e) are correct. \((N K=\) number of children in the household.)

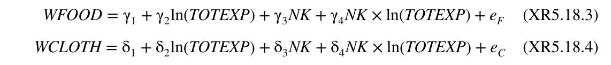
g. Compare the estimates for \(\partial E(W F O O D \mid \mathbf{X}) / \partial \ln (T O T E X P)\) from \((\mathrm{XR5.18.1)}\) for \(N K=1,2\) with those from (XR5.18.3) for \(N K=1,2\).

Data From Exercise 4.12:-

Consider the share of total household expenditure (TOTEXP) devoted to expenditure on food (FOOD). Specify the log-linear relationship FOOD/TOTEXP \(=\beta_{1}+\beta_{2} \ln (\) TOTEXP \()\).

a. Show that the elasticity of expenditure on food with respect to total expenditure is

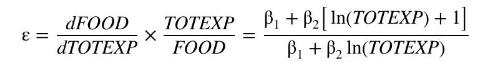
Solve the log-linear relationship as FOOD \(=\left[\beta_{1}+\beta_{2} \ln (\right.\) TOTEXP \(\left.)\right]\) TOTEXP and differentiate to obtain \(d F O O D / d T O T E X P\). Then multiply by TOTEXP/FOOD and simplify.]

b. The least squares estimates of the regression model FOOD/TOTEXP \(=\beta_{1}+\beta_{2} \ln (\) TOTEXP \()+e\), using 925 observations from London, are as follows:

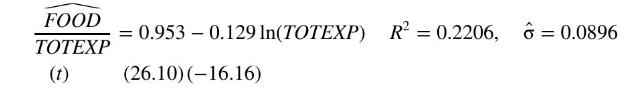
Interpret the estimated coefficient of \(\ln (T O T E X P)\). What happens to the share of food expenditure in the budget as total household expenditures increase?

c. Calculate the elasticity in part (a) at the 5th percentile, and the 75th percentile of total expenditure. Is this a constant elasticity function? The 5 th percentile is \(500 \mathrm{UK}\) pounds, and the 75 th percentile is 1200 UK pounds.

d. The residuals from the model in (b) have skewness 0.0232 and kurtosis 3.4042. Carry out the Jarque-Bera test at the \(1 \%\) level of significance. What are the null and alternative hypotheses for this test?

e. In FOOD/TOTEXP \(=\beta_{1}+\beta_{2} \ln (\) TOTEXP \()\), take the logarithm of the left-hand side and simplify the result to obtain \(\ln (F O O D)=\alpha_{1}+\alpha_{2} \ln (T O T E X P)\). How are the parameters in this model related to the budget share relation?
f. The least squares estimates of \(\ln (F O O D)=\alpha_{1}+\alpha_{2} \ln (\) TOTEXP \()+e\) are as follows:

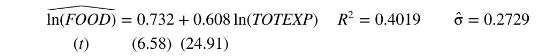
Interpret the estimated coefficient of \(\ln (T O T E X P)\). Calculate the elasticity in this model at the 5 th percentile and the 75th percentile of total expenditure. Is this a constant elasticity function?
g. The residuals from the log-log model in (e) show skewness \(=-0.887\) and kurtosis \(=5.023\). Carry out the Jarque-Bera test at the \(5 \%\) level of significance.
h. In addition to the information in the previous parts, we multiply the fitted value in part (b) by TOTEXP to obtain a prediction for expenditure on food. The correlation between this value and actual food expenditure is 0.641 . Using the model in part (e) we obtain \(\exp [\widehat{\ln (F O O D)}]\). The correlation between this value and actual expenditure on food is 0.640 . What if any information is provided by these correlations? Which model would you select for reporting, if you had to choose only one? Explain your choice.

Transcribed Image Text:

WFOOD B+ In(TOTEXP) + eF (XR5.19.1)