Consider the following two expenditure share equations where the budget share for food WFOOD, and the budget share for clothing WCLOTH, are expressed as functions of total expenditure TOTEXP.

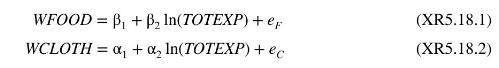
a. A commodity is regarded as a luxury if the coefficient of \(\ln (T O T E X P)\) is positive and a necessity if it is negative. What signs would you expect for \(\beta_{2}\) and \(\alpha_{2}\) ?

b. Using the data in the file london5, estimate the above equations using observations on households with one child. Comment on the estimates and their significance. Can you explain any possibly counterintuitive outcomes?

c. Using a \(1 \%\) significance level, test \(H_{0}: \beta_{2} \geq 0\) against the alternative \(H_{1}: \beta_{2}

d. Using a \(1 \%\) significance level, test \(H_{0}: \alpha_{2} \geq 0\) against the alternative \(H_{1}: \alpha_{2}

e. Estimate the two equations using observations on households with two children. Construct \(95 \%\) interval estimates for \(\beta_{2}\) and \(\alpha_{2}\) for both one- and two-child households. Based on these interval estimates, would you conjecture that the coefficients of \(\ln (T O T E X P)\) are the same or different for one- and two-child households.

f. Use all observations to estimate the following two equations and test, at a \(95 \%\) significance level, whether your conjectures in part (e) are correct. \((N K=\) number of children in the household.)

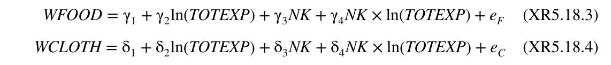
g. Compare the estimates for \(\partial E(W F O O D \mid \mathbf{X}) / \partial \ln (T O T E X P)\) from \((\mathrm{XR5.18.1)}\) for \(N K=1,2\) with those from (XR5.18.3) for \(N K=1,2\).

Transcribed Image Text:

= WFOOD B+ B2 In(TOTEXP) + eF WCLOTH= In(TOTEXP) + ec (XR5.18.1) (XR5.18.2)