Do larger universities have lower cost per student or a higher cost per student? Use the data

Question:

Do larger universities have lower cost per student or a higher cost per student? Use the data on 141 public universities in the data file pubcoll for 2010 and 2011. A university is many things and here we only focus on the effect of undergraduate full-time student enrollment (FTESTU) on average total cost per student (ACA). Consider the regression model \(A C A_{i t}=\beta_{1}+\beta_{2} F^{2} E S T U_{i t}+e_{i t}\) where the subscripts \(i\) and \(t\) denote the university and the time period, respectively. Here, \(e_{i t}\) is the usual random error term.

a. Estimate the model above using 2010 data only, again using 2011 data only, and again using both years of data together. What is the estimated effect of increasing enrollment on average cost per student? Base your answer on both point and 95\% interval estimates.

b. There are certainly many other factors affecting average cost per student. Some of them can be characterized as the university "identity" or "image." Let us denote these largely unobservable individual attributes as \(u_{i}\). If we could add this feature to the model, it would be \(A C A_{i t}=\beta_{1}+\beta_{2}\) FTESTU it \(_{i t}+\left(\theta u_{i}+e_{i t}\right)\). We place it in parentheses with \(e_{i t}\) because it is another unobservable random error, but it is different because the character or identify of a university does not change from one year to the next. Do you suppose that our usual exogeneity assumptions hold in light of this new class of omitted variables? Might some unobservable characteristics of a university be correlated with student enrollment? Give some examples.

c. With our two years of data, we can take "first differences," by subtracting the model in 2010 from the model in 2011, \(\triangle A C A_{i}=\beta_{2} \Delta F T E S T U_{i}+\Delta e_{i}\), where

image text in transcribed

Explain why the intercept and \(\theta u_{i}\) drop from the model. Explain how the exogeneity assumptions might now hold.

d. Estimate \(\triangle A C A_{i}=\beta_{2} \Delta\) FTESTU \(_{i}+\Delta e_{i}\) and also \(\triangle A C A_{i}=\delta+\beta_{2} \Delta F T E S T U_{i}+\Delta e_{i}\). What now is the estimated effect of increasing enrollment on average cost per student? Base your answer on both point and \(95 \%\) interval estimates. Does adding an intercept to the model make any fundamental difference in this case?

e. Estimate the model \(\Delta \ln \left(A C A_{i}\right)=\alpha+\gamma \Delta \ln \left(F F T E S T U_{i}\right)+\Delta e_{i}\) where

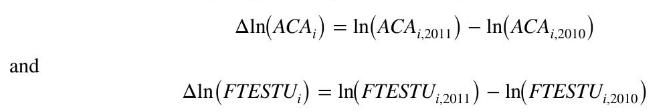
image text in transcribed