Reconsider the variables and model from Exercise 5.31

Suppose that Bill is mainly interested in the magnitude of the coefficient \(\beta_{2}\). He has control over his departure time, but no control over the red lights or the trains.

a. Regress DEPART on the variables REDS and TRAINS and save the residuals. Which coefficient estimates are significantly different from zero at a 5\% level? For the significant coefficient(s), do you think the relationship is causal?

b. Regress TIME on the variables REDS and TRAINS and save the residuals. Are the estimates for the coefficients of REDS and TRAINS very different from the estimates for \(\beta_{3}\) and \(\beta_{4}\) obtained by estimating the complete model with DEPART included?

c. Use the residuals from parts (a) and (b) to estimate the coefficient \(\beta_{2}\) and adjust the output to obtain its correct standard error.

Data From Exercise 5.31:-

Each morning between 6:30 AM and 8:00 AM Bill leaves the Melbourne suburb of Carnegie to drive to work at the University of Melbourne. The time it takes Bill to drive to work (TIME), depends on the departure time (DEPART), the number of red lights that he encounters (REDS), and the number of trains that he has to wait for at the Murrumbeena level crossing (TRAINS). Observations on these variables for the 249 working days in 2015 appear in the file commute5. TIME is measured in minutes. DEPART is the number of minutes after 6:30 AM that Bill departs.

a. Estimate the equation

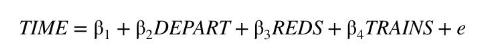
Report the results and interpret each of the coefficient estimates, including the intercept \(\beta_{1}\).

b. Find \(95 \%\) interval estimates for each of the coefficients. Have you obtained precise estimates of each of the coefficients?

c. Using a 5\% significance level, test the null hypothesis that Bill's expected delay from each red light is 2 minutes or more against the alternative that it is less than 2 minutes.

d. Using a \(10 \%\) significance level, test the null hypothesis that the expected delay from each train is 3 minutes against the alternative that it is not 3 minutes.

e. Using a 5\% significance level, test the null hypothesis that Bill can expect a trip to be at least 10 minutes longer if he leaves at 7:30 AM instead of 7:00 AM, against the alternative that it will not be 10 minutes longer. (Assume other things are equal.)

f. Using a 5\% significance level, test the null hypothesis that the expected delay from a train is at least three times greater than the expected delay from a red light against the alternative that it is less than three times greater.

g. Suppose that Bill encounters six red lights and one train. Using a 5\% significance level, test the null hypothesis that leaving Carnegie at 7:00 Am is early enough to get him to the university on or before 7:45 AM against the alternative that it is not. [Carry out the test in terms of the expected time \(E(T I M E \mid \mathbf{X})\) where \(\mathbf{X}\) represents the observations on all explanatory variables.]

h. Suppose that, in part (g), it is imperative that Bill is not late for his 7:45 AM meeting. Have the null and alternative hypotheses been set up correctly? What happens if these hypotheses are reversed?

Transcribed Image Text:

TIME = B1+DEPART + 3REDS + BTRAINS + e