The data file ozconfn contains quarterly data on Australian real consumption expenditure (CONS) and real net national disposable income (INC) from 1975Q1 to 2010Q4.

a. Create the series \(L C O N S=\ln (C O N S)\) and plot the series LCONS and INC. Comment on the graphs.

b. Detrend each of the series by estimating the linear trends \(\operatorname{LCONS}_{t}=a_{1}+a_{2} t+u_{1 t}\) and \(I N C_{t}=c_{1}+c_{2} t+u_{2 t}\), and saving the residuals. Use values \(t=0,1, \ldots, T-1\) for the trend term.

c. Plot the detrended series and comment on the graphs.

d. From part (c), you will have noticed that there is a strong seasonal component in each series. Econometricians have developed several methods for removing a seasonal component or "seasonally adjusting" the data. One very simple method is to subtract out the effect of seasonal dummy variables. To use this method, and remove the trend at the same time, we estimate the equation

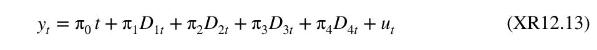
where \(D_{j t}=1\) when \(t\) is an observation in quarter \(j\), and 0 otherwise. Estimate (XR12.13) for both \(L C O N S\) and \(I N C\) and save the residuals; call them \(L C O N S^{*}\) and \(I N C^{*}\).

e. Plot \(L C O N S^{*}\) and \(I N C^{*}\) and compare these graphs with those obtained in part (c).

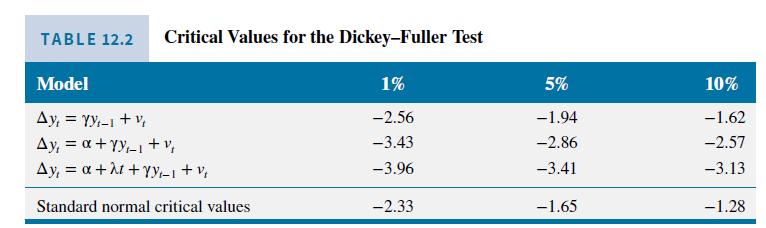
f. Using a 5\% significance level and the critical values in the third row of Table 12.2, test whether \(\operatorname{LCONS}^{*}\) and \(I N C^{*}\) are stationary or first-difference stationary. Explain your choice of test equation, and comment on the suitability of the critical values.
g. Estimate the following two equations and compare the estimates \[
\begin{aligned}
& \operatorname{LCONS}_{t}=\delta t+\phi_{1} D_{1 t}+\phi_{2} D_{2 t}+\phi_{3} D_{3 t}+\phi_{4} D_{4 t}+\beta I N C_{t}+e_{t} \\
& \operatorname{LCONS}_{t}^{*}=\beta I N C_{t}^{*}+e_{t}
\end{aligned}
\]
h. Using a 5\% significance level, test whether the equation in part (g)-either equation-is a cointegrating relationship. What critical value did you use?
i. Estimate an error correction model relating \(\triangle L C O N S_{t}\) to \(\Delta I N C_{t}\) and, if relevant, the lagged cointegrating residuals from part \((\mathrm{g})\).

Data From Table 12.2:-

Transcribed Image Text:

y =ot+D +D21+3D31 + 4 D + u 41 (XR12.13)