There were 64 countries who competed in the 1992 Olympics and won at least one medal. For

Question:

There were 64 countries who competed in the 1992 Olympics and won at least one medal. For each of these countries, let MEDALS be the total number of medals won, $P O P M$ be population in millions, and GDPB be GDP in billions of 1995 dollars. Excluding the United Kingdom, and using $N=63$ observations, the model MEDALS $=\beta_{1}+\beta_{2} \ln (P O P M)+\beta_{3} \ln (G D P B)+e$ was estimated as

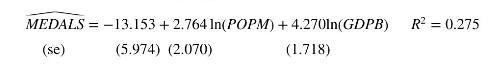
image text in transcribed

a. Given assumptions MR1-MR6 hold, interpret the coefficient estimates for $\beta_{2}$ and $\beta_{3}$.

b. Interpret $R^{2}$.

c. Using a $10 \%$ significance level, test the hypothesis that there is no relationship between the number of medals won and GDP against the alternative that there is a positive relationship. What happens if you change the significance level to $5 \%$ ?

d. Using a $10 \%$ significance level, test the hypothesis that there is no relationship between the number of medals won and population against the alternative that there is a positive relationship. What happens if you change the significance level to 5\%?

e. Use the model to find point and $95 \%$ interval estimates for the expected number of medals won by the United Kingdom whose population and GDP in 1992 were 58 million and $\$ 1010$ billion, respectively. [The standard error for $b_{1}+\ln (58) \times b_{2}+\ln (1010) \times b_{3}$ is 4.22196.]

f. The United Kingdom won 20 medals in 1992. Is the model a good one for predicting the mean number of medals for the United Kingdom? What is an approximate $p$-value for a test of $H_{0}: \beta_{1}+\ln (58) \times \beta_{2}+\ln (1010) \times \beta_{3}=20$ versus $H_{1}: \beta_{1}+\ln (58) \times \beta_{2}+\ln (1010) \times \beta_{3} eq 20$ ?
g. Without doing any of the calculations, write down the expression that is used to compute the standard error given in part (e).

Fantastic news! We've Found the answer you've been seeking!