Using data from 1950 to 1996 ( \(T=47\) observations), the following equation for explaining wheat yield in the Mullewa Shire of Western Australia was estimated as

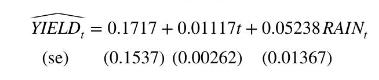
where \(Y I E L D_{t}=\) wheat yield in tonnes per hectare in year \(t\);
\(T_{R E N D}^{t}\) is a trend variable designed to capture technological change, with observations \(t=1,2, \ldots, 47\)
\(R A I N_{t}\) is total rainfall in inches from May to October (the growing season) in year \(t\). The sample mean and standard deviation for RAIN are \(\bar{x}_{\text {RAIN }}=10.059\) and \(s_{\text {RAIN }}=2.624\).

a. Given assumptions MR1-MR5 hold, interpret the estimates for the coefficients of \(t\) and RAIN.

b. Using a \(5 \%\) significance level, test the null hypothesis that technological change increases mean yield by no more than 0.01 tonnes per hectare per year against the alternative that the mean yield increase is greater than 0.01.

c. Using a 5\% significance level, test the null hypothesis that an extra inch of rainfall increases mean yield by 0.03 tonnes per hectare against the alternative that the increase is not equal to 0.03.

d. Adding \(R A I N^{2}\) to the equation and reestimating yields

What is the rationale for including RAIN \(^{2}\) ? Does it have the expected sign?

e. Repeat part (b) using the model estimated in (d).

f. Repeat part (c) using the model estimated in (d), testing the hypothesis at the mean value of rainfall. (The estimated covariance between \(b_{3}\) and \(b_{4}\) (the coefficients of RAIN and RAIN \({ }^{2}\) ) is \(\widehat{\operatorname{cov}}\left(b_{3}, b_{4}\right)=-0.0002493\).

g. Use the model in (d) to forecast yield in 1997, when the rainfall was 9.48 inches.

h. Suppose that you wanted to forecast 1997 yield before the rainfall was observed. What would be your forecast from the model in (a)? What would it be from the model in (d)?

Transcribed Image Text:

YIELD, = 0.1717 +0.01117++ 0.05238 RAIN, (se) (0.1537) (0.00262) (0.01367)