This exercise examines a supply and demand model for edible chicken, which the U.S. Department of Agriculture calls "broilers." The data for this exercise are in the file newbroiler, which is adapted from the data provided by Epple and McCallum (2006). We considered the demand equation in Exercise 11.20. The supply equation is

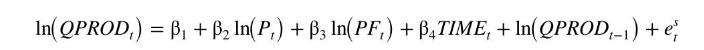
where \(Q P R O D\) is the aggregate production of young chickens, \(P F\) is nominal price index of broiler feed, and TIME = time index with \(1950=1, \ldots, 2001=52\). This supply equation is dynamic, with lagged production on the right-hand side. This predetermined variable is exogenous. TIME is included to capture technical progress in production.

a. What are the endogenous variables? What are the exogenous variables? What is the interpretation of the parameter \(\beta_{2}\) ? What signs do you expect for each of the parameters?

b. Using data from 1960 to 1999 , estimate the supply equation by OLS. Comment on the signs and significance of the estimates. Test the residuals for serial correlation. Is serial correlation present?

c. Estimate the reduced-form, first-stage, regression by OLS using the IVs \(\ln \left(Y_{t}\right), \ln \left(P B_{t}\right), P O P G R O\), and \(\ln \left(E X P T S_{t-1}\right)\). Test the joint significance of these variables. Can we conclude that we have at least one strong instrument?

d. Estimate the supply equation by 2SLS using the instruments listed in part (c). Compare and contrast these results to those in part (b).

e. Test the validity of the surplus instruments using the Sargan test, discussed in Section 10.4.3.

Data From Exercise 11.20:-

This exercise examines a supply and demand model for edible chicken, which the U.S. Department of Agriculture calls "broilers." The data for this exercise are in the file newbroiler, which is adapted from the data provided by Epple and McCallum (2006). We consider the demand equation in this exercise and the supply equation in Exercise 11.21.

a. Consider the demand equation:

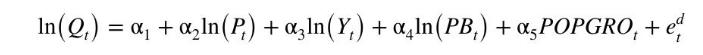
where \(Q=\) per capita consumption of chicken, in pounds; \(Y=\) real per capita income; \(P=\) real price of chicken; \(P B=\) real price of beef; and \(P O P G R O=\) rate of population growth. What are the endogenous variables? What are the exogenous variables?

b. Using data from 1960 to 1999 , estimate the demand equation by OLS. Comment on the signs and significance of the estimates.

c. Test the OLS residuals from part (b) for serial correlation by constructing a correlogram and carrying out the \(T \times R^{2}\) test. What do you conclude about the presence of serial correlation?

d. Estimate the demand equation by 2SLS using as instruments \(\ln \left(P F_{t}\right), T I M E_{t}=Y E A R_{t}-1949\), \(\ln \left(Q P R O D_{t-1}\right)\), and \(\ln \left(E X P T S_{t-1}\right)\). Compare and contrast these estimates to the OLS estimates in part (a).

e. Estimate the reduced-form, first-stage, equation and test the joint significance of \(\ln \left(P F_{t}\right), T I M E_{t}\), \(\ln \left(Q P R O D_{t-1}\right)\), and \(\ln \left(E X P T S_{t-1}\right)\). Can we conclude that at least one instrument is strong?

f. Test the reduced-form equation for serial correlation using the \(T \times R^{2}\) test.

g. Estimate the reduced-form, first-stage, equation using HAC standard errors and test the joint significance of \(\ln \left(P F_{t}\right), T I M E_{t}, \ln \left(\right.\) QPROD \(\left._{t-1}\right)\), and \(\ln \left(E X P T S_{t-1}\right)\).

h. Obtain the 2SLS residuals from part (d). Construct a correlogram. Is there evidence of serial correlation? Obtain 2SLS estimates with HAC standard errors and compare the results to those in (d).

i. Test the validity of the surplus instruments using the Sargan test, discussed in Section 10.4.3, and the 2SLS estimates in part (d).

Transcribed Image Text:

In(QPROD,) = B + 2 In(P,) + 3 In(PF) + BTIME, + In(QPROD-1) + e,