We have five observations on \(x\) and \(y\). They are \(x_{i}=3,2,1,-1,0\) with corresponding \(y\) values \(y_{i}=4,2,3,1,0\). The fitted least squares line is \(\hat{y}_{i}=1.2+0.8 x_{i}\), the sum of squared least squares residuals is \(\sum_{i=1}^{5} \hat{e}_{i}^{2}=3.6\) and \(\sum_{i=1}^{5}\left(y_{i}-\bar{y}\right)^{2}=10\). Carry out this exercise with a hand calculator.

a. Calculate the fitted values \(\hat{y}_{i}\) and their sample mean \(\overline{\hat{y}}\). Compare this value to the sample mean of the \(y\) values.

b. Calculate \(\sum_{i=1}^{5}\left(\hat{y}_{i}-\bar{y}\right)^{2}\) and \(\sum_{i=1}^{5}\left(\hat{y}_{i}-\bar{y}\right)^{2} / \sum_{i=1}^{5}\left(y_{i}-\bar{y}\right)^{2}\).

c. The least squares residuals are \(\hat{e}_{i}=0.4,-0.8,1,0.6\), and -1.2 . Calculate \(\sum_{i=1}^{5}\left(\hat{y}_{i}-\bar{y}\right) \hat{e}_{i}\).

d. Calculate \(1-\sum_{i=1}^{5} \hat{e}_{i}^{2} / \sum_{i=1}^{5}\left(y_{i}-\bar{y}\right)^{2}\) and compare it to the results in part (b).

e. Show, algebraically, that \(\sum_{i=1}^{5}\left(\hat{y}_{i}-\bar{y}\right)\left(y_{i}-\bar{y}\right)=\sum_{i=1}^{5} \hat{y}_{i} y_{i}-N \bar{y}^{2}\). Calculate this value.

f. Using \(\sum_{i=1}^{5}\left(x_{i}-\bar{x}\right)^{2}=10\), and previous results, calculate

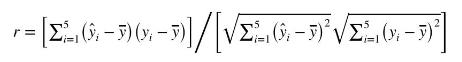
What statistic is \(r\) ? Calculate \(r^{2}\) and compare this value to the values in parts (d) and (b).

Transcribed Image Text:

r = i=] i=1 2