A marketed asset's price \(x\) is governed by the mean reverting process

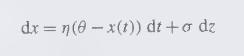
where \(\eta, \theta\), and \(\sigma\) are positive constants and \(z\) is a Wiener process.

(a) Let \(V(x, t)\) be a given function. Find the Ito process that governs \(V\).

(b) Suppose also that there is a marketed bond satisfying \(\mathrm{d} B(t)=r B(t) \mathrm{d} t\) with \(r>0\). Let \(V(x, t)\) be the value of a derivative of \(x\) and \(B\). Using the pricing axioms, find the partial differential equation governing \(V\).

Transcribed Image Text:

dx = n(6-x(t)) dt + dz ==