Assume we have a non-dividend-paying stock governed by the stochastic differential equation \(\mathrm{d} S_{t}=\mu S_{t} \mathrm{~d} t+\sigma S_{t} \mathrm{~d} z_{t}\) and a risk-free asset carrying a fixed interest rate \(r\). The value \(B\) of the risk-free asset satisfies \(\mathrm{d} B=r B \mathrm{~d} t\). Consider a European contract that pays the \(k\) th power (where \(k\) is a positive integer) of the stock at time T. It can be shown that the price of the contract at time \(\mathrm{t}(t \leq T)\) has the form

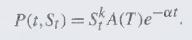
Find \(A(T)\) and \(\alpha\) explicitly.

Transcribed Image Text:

P(t,S,) = SA(T)eat