As with Exercise 10, the sensitivity of a derivative asset with respect to the underlying interest rate \(r\) is termed rho and defined as

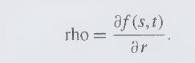
For a call option on stock following the Black-Scholes framework, rho \(=K T e^{-r T} N\left(d_{2}\right)\), where \(d_{2}\) is defined by equation \((15.16 c)\). What is the value of rho for the corresponding put? [Express in terms of \(N\left(-d_{2}\right)\).]

Data from Exercises 10

For a derivative of an asset that follows standard geometric Brownian motion, it may be useful to find the sensitivity of the derivative price with respect to a parameter of the underlying process. In particular, for the parameter \(\sigma\) the corresponding sensitivity is termed vega and is

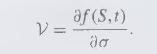
For a call option on stock that follows geometric Brownian motion there holds \(\mathcal{V}=S \sqrt{T} N^{\prime}\left(d_{1}\right)\), where \(d_{1}\) is given by equation \((15.16 b)\). What is vega for the corresponding put option?

Transcribed Image Text:

af (s,t) rho = r