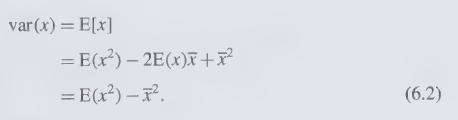Consider a general betting wheel with \(n\) segments. The pay off for a \(\$ 1\) bet on a segment \(i\) is \(A_{i}\). Suppose you bet an amount \(B_{i}=1 / A_{i}\) on segment \(i\) for each \(i\). Show that the amount you win is independent of the outcome of the wheel. What is the risk-free rate of return for the wheel? Apply this to the wheel in Example 6.7.

Equations

Transcribed Image Text:

Example 6.7 (Betting wheel) Two kinds of wheels are useful for the study of investment problems. The wheel of fortune of Example 6.5 is one form of wheel. For that type, one bets on (invests in) the wheel as a whole, and the payoff is determined by the landing segment. The other kind of wheel is a betting wheel, an example of which is shown in Figure 6.5. For this kind of wheel one bets on (invests in) the individual segments of the wheel. For example, for the wheel shown, if one invests $1 in the white segment, then $3 will be the payoff if white is the landing segment; otherwise the payoff is zero and the original $1 is lost. One is allowed to bet different amounts on different segments. A roulette wheel is a betting wheel. From a theoretical viewpoint, a betting wheel is interesting because the returns from different segments are correlated. For the wheel shown, we may bet on: (1) white, (2) black, or (3) gray, with payoffs 3, 2, or 6, respectively. Note that the bet on white has quite favorable odds. We can work out the expected rates of return for the three possible bets. It is much easier here to work first with total returns and then subtract 1. For example, for white the return is 3 with probability and 0 with probability The three expected values are: R = (3)+(0) = R = (2)+(0)= R3 = (6)+(0)=1.