Consider a stock price \(S\) governed by the geometric Brownian motion process

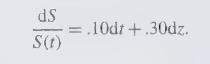
(a) Using \(\Delta t=1 / 12\) and \(S(0)=1\), simulate several (i.e., many) years of this process using either method, and evaluate \[
\frac{1}{t} \ln [S(t)]
\]
as a function of \(t\). Note that it tends to a limit \(p\). What is the theoretical value of this limit?

(b) About how large must \(t\) be to obtain two-place accuracy?

(c) Evaluate \[
\frac{1}{t}[\ln S(t)-p t]^{2}
\]
as a function of \(t\). Does this tend to a limit? If so, what is its theoretical value?

Transcribed Image Text:

S(t) =.10dt +.30dz. SP