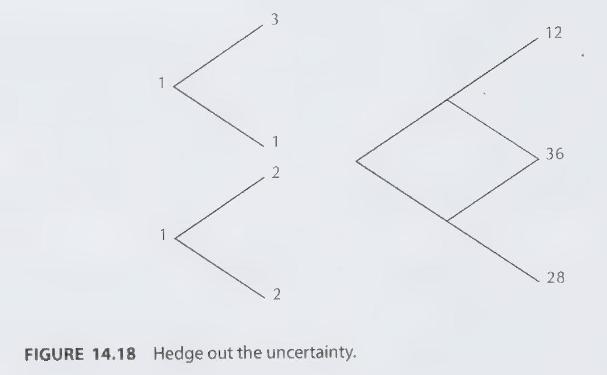
Consider the stock and bond lattices on the left of Figure 14.18. Each has unit cost of \(\$ 1\) with the payoffs shown at the end nodes. There is a new asset available-a derivative of the first two - with the payoffs shown at the end of two periods, as indicated in the lattice on the right side of the figure.

(a) Find the value of this new asset.

(b) What is the deterministic payoff that should be obatined at the end of two periods?

(c) Show how to hedge this new asset by trading the stock and the bond in such a way that the deterministic payoff is obtained. [Hint: Construct a lattice with payoffs 16 , -8 , and 0 , and argue that it should cost 0 . Solve for the resulting values at each node. Next work forward using a self-fiancing portfolio to match the node values. You may like to remember that to match in a binary lattice we set \(x=\left(\mathrm{Cu}-\mathrm{C}_{d}\right) /\) \((u-d)\).

Transcribed Image Text:

2 3 FIGURE 14.18 Hedge out the uncertainty. 12 36 28