Suppose that revenue has the form where (h) can be chosen and (x) and (y) are random

Question:

Suppose that revenue has the form

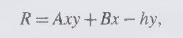
image text in transcribed

where $h$ can be chosen and $x$ and $y$ are random variables. The distribution of $x$ and $y$ is symmetric about $(0,0)$; that is, $-x,-y$ has the same distribution as $x, y$. Show that the choice of $h$ that minimizes the variance of $R$ is

image text in transcribed

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Investment Science

ISBN: 9780199740086

2nd Edition

Authors: David G. Luenberger

See More Books

Question Posted: Apr 20, 2024 12:00 PM

See More Questions

CANMNMM January of this year. (a) Each item will be held in a record. Describe all the data structures that must refer to these records to implement the required functionality. Describe all the...
Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...
Mr. Banks is a CEO of an airline parts company. In negotiating with a major customer, he asks many questions and carefully summarized the other parties' ideas. This is an example of which effective...
On January 1, 2012, Piranto acquires 90 percent of Slinton's outstanding shares. Financial information for these two companies for the years of 2012 and 2013 follows: Assume that a tax rate of 40...
Given that has eigenvector find the corresponding eigenvalue and the value of a. Hence, find the remaining eigenvalues and eigenvectors. 1 5 7\ A = 1 3 -1 5/
Consider a Poisson regression. Let $e_{i}=y_{i}-\widehat{\mu}_{i}$ denote the $i$ th ordinary residual. Assume that an intercept is used in the model so that one of the explanatory variables...
Figure 5.4 shows that CBSs five-year borrowing rate is 1.3% and JPMorgan Chases is 2.6%. Which would you prefer? $500 from CBS paid today or a promise that the firm will pay you $550 in five years?...
BRIGHTLIGHT INC. manufactures lamps and expects to sell 3 5 0 , 0 0 0 units next year at $ 2 1 per unit. Planned per - unit manufacturing costs at that level of production are as follows: Variable $...
Suppose that, as in the corn farm example, the farm has random production and the final spot price is governed by the same demand function. However, the crop of the farm is not perfectly correlated...
Suppose the wealth that is to be received at a time $T$ in the future has the form where $a$ is a constant and $x$ is a random variable. The value of the variable $h$ can be selected by the...
Given the Keynesian explanation for the persistence of high levels of unemployment after the recessions of the early 1980s and early 1990s, what policies would you advocate to reduce unemployment in...
Explain the way in which the debt-to- income/ payment-to-income ratio and the loan-to value ratio are used to assess a potential borrower's, suitability to receive a mortgage loan.
List and explain 4 characteristics of a bond that are attractive to investors.
The face value for zero coupon bond is $100000 and the bond matures in 30 years. Suppose that the appropriate discount rate is 7% per year with annual compounding m. What price are we willing to pay...
How to calculate the ratio Analysis (liquidity, leverage, activity, profitability, coverage ratios) for income statement, balance sheet and cash flow statements for Nike 2020,2019 & Pepsico 2019,2018?
Explain how a company could (a) improve its credit rating withsuppliers after paying some late; (b) lower its cost of financing when the market interest rate has increased. (financial magmt)
A perfectly plane house roof makes an angle - with the horizontal. When its temperature changes, between Tc before dawn each day to Th in the middle of each afternoon, the roof expands and contracts...
Calculate Total Contribution Margin for the same items. Total Revenue Total Variable Costs Total Contribution Margin $50.00 a. $116.00 $329.70 b. $275.00 $14,796.00 $7,440.00 c. $40,931.25 d....
Interest rates have a huge impact on the national and global economy, as well as for specific business practices.Visit the website of a local bank and see what rates are being applied to business...
In building a storage shed, workers use nails from a large bin. The bin is suspended from a vertical spring twice during the day to measure the usage of nails. At the beginning of the day, the spring...
Robin, who is self - employed, contributes $ 4 0 0 0 / year into a Keogh account. How much will he have in the account after 2 5 years if the account earns interest at the rate of 5 . 5 % / year...

Suppose that revenue has the form where (h) can be chosen and (x) and (y) are random

Question:

R=Axy+Bx-hy,

Step by Step Answer:

Investment Science

Students also viewed these Business questions